题目内容
已知函数f(x)=2sin(x-
).
(1)求函数f(x)图象的对称轴方程和函数x(x)的单调增区间;
(2)求函数y=f(x)的图象与直线y=2的两个相邻交点的距离.
| π |
| 6 |
(1)求函数f(x)图象的对称轴方程和函数x(x)的单调增区间;
(2)求函数y=f(x)的图象与直线y=2的两个相邻交点的距离.
考点:正弦函数的图象
专题:三角函数的图像与性质
分析:(1)根据三角函数单调性,对称性的计算公式即可得到结论.
(2)根据三角函数性质转化为求函数的周期即可.
(2)根据三角函数性质转化为求函数的周期即可.
解答:
解:(1)由-
+2kπ≤x-
≤
+2kπ,
解得-
+2kπ≤x≤
+2kπ,
即函数的递增区间为[-
+2kπ,
+2kπ],k∈Z,
由x-
=2kπ+
,即x=
+2kπ,k∈Z,
即函数的对称轴为x=
+2kπ,k∈Z.
(2)由f(x)=2,得2sin(x-
)=2.
即sin(x-
)=1
则函数y=f(x)的图象与直线y=2的两个相邻交点的距离为一个周期T,
则T=
=2π.
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解得-
| π |
| 3 |
| 2π |
| 3 |
即函数的递增区间为[-
| π |
| 3 |
| 2π |
| 3 |
由x-
| π |
| 6 |
| π |
| 2 |
| 2π |
| 3 |
即函数的对称轴为x=
| 2π |
| 3 |
(2)由f(x)=2,得2sin(x-
| π |
| 6 |
即sin(x-
| π |
| 6 |
则函数y=f(x)的图象与直线y=2的两个相邻交点的距离为一个周期T,
则T=
| 2π |
| 1 |
点评:本题主要考查三角函数的图象和性质,要求熟练掌握函数单调性,周期性以及对称性的求解.

练习册系列答案
相关题目
已知向量
=(-1,x),
=(1,x),若2
-
与
垂直,则|a|=( )
| a |
| b |
| b |
| a |
| a |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、4 |
 如图,正方体ABCD-A1B1C1D1的棱长是2,点E、F分别是两条棱的中点
如图,正方体ABCD-A1B1C1D1的棱长是2,点E、F分别是两条棱的中点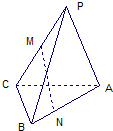 如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.求证:MN⊥AB.
如图P是△ABC所在平面外一点,PA=PB,CB⊥平面PAB,M是PC的中点,N是AB上的点,AN=3NB.求证:MN⊥AB.