题目内容
已知函数y=loga(x+3)+6(a>0,a≠1)的图象恒过定点M,椭圆G:
+
=1(a>b>0)的左,右焦点分别为F1,F2,直线l经过点M且与⊙C:x2+y2+2x-6y+9=0相切.
(1)求直线l的方程;
(2)若直线l经过点F2并与椭圆G在x轴上方的交点为P,且cos∠F1PF2=
,求△PF1F2内切圆的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求直线l的方程;
(2)若直线l经过点F2并与椭圆G在x轴上方的交点为P,且cos∠F1PF2=
| 7 |
| 25 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)函数y=loga(x+3)+6(a>0,a≠1)的图象恒过定点M(-2,6),⊙C的圆心为C(-1,3),半径r=1.对切线的斜率分类讨论,利用点到直线的距离公式与切线的性质即可得出.
(2)设∠F1PF2=α,∠F1F2P=β,则由cosα=
,得sinα=
.又由直线l的斜率为k=-
,可得sin∠PF1F2=
.有∠PF1F2=β,△F1PF2是等腰三角形,点P是椭圆的上顶点.易知P(0,
). 于是△PF1F2内切圆的圆心D在线段PO上.设D(0,m),内切圆半径为r.则0<m<
,r=m.解出即可.
(2)设∠F1PF2=α,∠F1F2P=β,则由cosα=
| 7 |
| 25 |
| 24 |
| 25 |
| 4 |
| 3 |
| 4 |
| 5 |
| 10 |
| 3 |
| 10 |
| 3 |
解答:
解:(1)函数y=loga(x+3)+6(a>0,a≠1)的图象恒过定点M(-2,6),
⊙C的圆心为C(-1,3),半径r=1.
①当l⊥x轴时,l的方程为x+2=0,易知l和⊙C相切.
②当l与x轴不垂直时,设l的方程为y-6=k(x+2),即kx-y+2k+6=0,
圆心C(-1,3)到l的距离为d=
.
由l和⊙C相切,得
=1,解得k=-
.
于是l的方程为4x+3y-10=0.
综上,得直线l的方程为x+2=0,或4x+3y-10=0.
(2)设∠F1PF2=α,∠F1F2P=β,则由cosα=
,得sinα=
.
又由直线l的斜率为k=-
,得sinβ=
,cosβ=
.
于是sin∠PF1F2=sin(α+β)=sinαcosβ+cosαsinβ=
×
+
×
=
.
有∠PF1F2=β,△F1PF2是等腰三角形,点P是椭圆的上顶点.
易知P(0,
).
于是△PF1F2内切圆的圆心D在线段PO上.
设D(0,m),内切圆半径为r.则0<m<
,r=m.
由点D到直线l的距离d=
=r=m,解得m=
.
故△PF1F2内切圆的方程为x2+(y-
)2=
.
⊙C的圆心为C(-1,3),半径r=1.
①当l⊥x轴时,l的方程为x+2=0,易知l和⊙C相切.
②当l与x轴不垂直时,设l的方程为y-6=k(x+2),即kx-y+2k+6=0,
圆心C(-1,3)到l的距离为d=
| |k+3| | ||
|
由l和⊙C相切,得
| |k+3| | ||
|
| 4 |
| 3 |
于是l的方程为4x+3y-10=0.
综上,得直线l的方程为x+2=0,或4x+3y-10=0.
(2)设∠F1PF2=α,∠F1F2P=β,则由cosα=
| 7 |
| 25 |
| 24 |
| 25 |
又由直线l的斜率为k=-
| 4 |
| 3 |
| 4 |
| 5 |
| 3 |
| 5 |
于是sin∠PF1F2=sin(α+β)=sinαcosβ+cosαsinβ=
| 24 |
| 25 |
| 3 |
| 5 |
| 7 |
| 25 |
| 4 |
| 5 |
| 4 |
| 5 |
有∠PF1F2=β,△F1PF2是等腰三角形,点P是椭圆的上顶点.
易知P(0,
| 10 |
| 3 |
于是△PF1F2内切圆的圆心D在线段PO上.
设D(0,m),内切圆半径为r.则0<m<
| 10 |
| 3 |
由点D到直线l的距离d=
| |3m-10| |
| 5 |
| 5 |
| 4 |
故△PF1F2内切圆的方程为x2+(y-
| 5 |
| 4 |
| 25 |
| 16 |
点评:本题考查了椭圆与圆的标准方程及其性质、直线与圆相切问题、斜率计算公式、点到直线的距离公式、三角形的内切圆的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
集合A={x∈N|3<x<9},B={3,5,7,8},则A∪B中的元素的个数有( )
| A、0 | B、2 | C、4 | D、6 |
下列函数中,满足f(xy)=f(x)+f(y)的单调递增函数是( )
| A、f(x)=log2x | ||
| B、f(x)=x2 | ||
| C、f(x)=2x | ||
D、f(x)=log
|
在平面直角坐标系中,定义两点P(x1,y1)与Q(x2,y2)之间的“直角距离”为d(P,Q)=|x1-x2|+|y1-y2|.给出下列命题:
(1)若P(1,2),Q(sinα,cosα)(α∈R),则d(P,Q)的最大值为3-
;
(2)若P,Q是圆x2+y2=1上的任意两点,则d(P,Q)的最大值为2
;
(3)若P(1,3),点Q为直线y=2x上的动点,则d(P,Q)的最小值为
.
其中为真命题的是( )
(1)若P(1,2),Q(sinα,cosα)(α∈R),则d(P,Q)的最大值为3-
| 2 |
(2)若P,Q是圆x2+y2=1上的任意两点,则d(P,Q)的最大值为2
| 2 |
(3)若P(1,3),点Q为直线y=2x上的动点,则d(P,Q)的最小值为
| 1 |
| 2 |
其中为真命题的是( )
| A、(1)(2)(3) |
| B、(2) |
| C、(3) |
| D、(2)(3) |
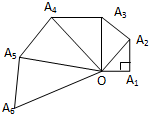 如图OA1=1,直角三角形OAnAn+1(n=1,2,3…)的直角边AnAn+1=
如图OA1=1,直角三角形OAnAn+1(n=1,2,3…)的直角边AnAn+1=| n |
A、an=
| ||||
B、an=
| ||||
C、an=
| ||||
D、an=
|
若不等式ax2+bx+c<0的解集为{x|x<0或x>β},(α<β<0),则不等式cx2-bx+a>0的解集为( )
A、{x|-
| ||||
B、{x|
| ||||
C、{x|-
| ||||
D、{x|x<-
|