题目内容
16.《孙子算经》是我国古代重要的数学著作,约成书于四、五世纪,传本的《孙子算经》共三卷,其中下卷:“物不知数”中有如下问题:“今有物,不知其数,三三数之,剩二;五五数之,剩三;七七数之,剩二,问:物几何?”其意思为:“现有一堆物品,不知它的数目,3个3个数,剩2个,5个5个数,剩3个,7个7个数,剩2个,问这堆物品共有多少个?”试计算这堆物品至少有23个.分析 根据“三三数之剩二,五五数之剩三,七七数之剩二”找到三个数:第一个数能同时被3和5整除;第二个数能同时被3和7整除;第三个数能同时被5和7整除,将这三个数分别乘以被7、5、3除的余数再相加即可求出答案.
解答 解:我们首先需要先求出三个数:
第一个数能同时被3和5整除,但除以7余1,即15;
第二个数能同时被3和7整除,但除以5余1,即21;
第三个数能同时被5和7整除,但除以3余1,即70;
然后将这三个数分别乘以被7、5、3除的余数再相加,即:15×2+21×3+70×2=233.
最后,再减去3、5、7最小公倍数的整数倍,可得:233-105×2=23,或者105k+23(k为正整数).
∴这堆物品至少有23,
故答案为:23.
点评 本题考查的是带余数的除法,简单的合情推理的应用,根据题意下求出15、21、70这三个数是解答此题的关键,属于中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
7.下列函数中,既是偶函数又在(0,+∞)上单调递减的是( )
| A. | y=-x | B. | y=cosx | C. | y=${x^{\frac{2}{5}}}$ | D. | y=-x2 |
8.某几何体的三视图如图所示,则该几何体的体积为( )
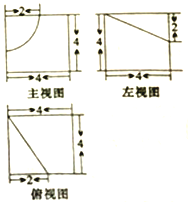

| A. | 64 | B. | 64-4π | C. | 64-8π | D. | 64-$\frac{4π}{3}$ |
5.化简sin2(2π-α)+cos(π+α)cos(π-α)+1( )
| A. | 0 | B. | 2sin2α+1 | C. | 2cos2α+1 | D. | 2 |
6.已知函数f(x)=(x3+2x2+ax-a)ex,f′(x)为f(x)的导函数,则f′(0)的值为( )
| A. | 0 | B. | 1 | C. | -a | D. | 不确定 |
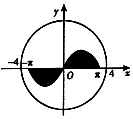 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.