题目内容
1.已知定义在(-∞,4]上的函数f(x)与其导函数f'(x)满足(x-1)(x-4)[f'(x)-f(x)]<0,若$f({|x|+|y|+1})-{e^{\frac{1}{2}|x|-1}}f({\frac{1}{2}|x|+|y|+2})<0$,则点(x,y)所在区域的面积为( )
| A. | 12 | B. | 6 | C. | 18 | D. | 9 |
分析 先构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,利用导数判断函数的单调性,利用函数的单调性则原不等式可转化为$\left\{\begin{array}{l}{-2<x<2}\\{|x|+|y|≤3}\\{|x|+2|y|≤4}\end{array}\right.$,画出相对应的可行域,求出影音部分的面积即可.
解答 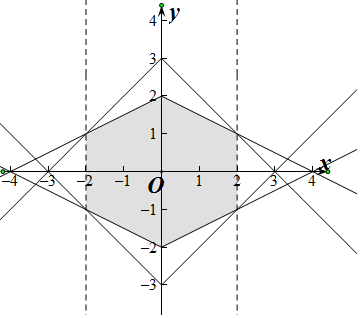 解:构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,
解:构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,
则g′(x)=$\frac{f′(x){e}^{x}-f(x){e}^{x}}{({e}^{x})^{2}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$,
又(x-1)(x-4)[f'(x)-f(x)]<0,
当x<1时,f'(x)-f(x)<0,
当1<x<4时,f'(x)-f(x)>0,
∴g(x)在(-∞,1)上单调递减,
在[1,4]上单调递增,
∵$f({|x|+|y|+1})-{e^{\frac{1}{2}|x|-1}}f({\frac{1}{2}|x|+|y|+2})<0$,
∴f(|x|+|y|+1)<${e}^{\frac{1}{2}|x|-1}$f($\frac{1}{2}$|x|+|y|+2),
同除以e|x|+|y|+1,
∴$\frac{f(|x|+|y|+1)}{{e}^{|x|+|y|+1}}$<$\frac{f(\frac{1}{2}|x|+|y|+2)}{{e}^{\frac{1}{2}|x|+|y|+2}}$,
∴g(|x|+|y|+1)<g($\frac{1}{2}$|x|+|y|+2),
∵|x|+|y|+1≥1,$\frac{1}{2}$|x|+|y|+2≥2,
∴|x|+|y|+1<$\frac{1}{2}$|x|+|y|+2,
即$\frac{1}{2}$|x|<1,
∴|x|<2,①
又定义域限制
∴|x|+|y|+1≤4,②
$\frac{1}{2}$|x|+|y|+2≤4,③,
∴$\left\{\begin{array}{l}{-2<x<2}\\{|x|+|y|≤3}\\{|x|+2|y|≤4}\end{array}\right.$,
画出如图所比表示的可行域,
∴S阴影=2S梯形=2×$\frac{1}{2}$×(2+4)×2=12,
故选:A
点评 本题考查了导数和函数的单调性的应用以及不等式的解法,考查了学生的转化能力,数形结合的能力,属于难题

| A. | $\frac{28}{3}$ | B. | $\frac{128}{9}$ | C. | $\frac{128}{8}\sqrt{3}$ | D. | $\frac{28}{3}\sqrt{2}$ |
 一个几何体的三视图如图所示,该几何体的表面积为( )
一个几何体的三视图如图所示,该几何体的表面积为( )| A. | 24-π | B. | 24-3π | C. | 24+π | D. | 24-2π |
| A. | $\frac{{\sqrt{7}}}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{{5\sqrt{7}}}{16}$ | D. | $\frac{9}{16}$ |
| A. | 4+2$\sqrt{3}$i | B. | -2+2$\sqrt{3}$i | C. | 4-2$\sqrt{3}$i | D. | -2-2$\sqrt{3}$i |