题目内容
6．
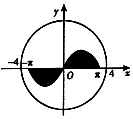如图，圆O：x2+y2=16内的正弦曲线y=sinx，x∈[-π，π]与x轴围成的区域记为M（图中阴影部分），随机向圆O内投一个点A，则点A落在区域M外的概率是1-$\frac{1}{4π}$．
分析 先求构成试验的全部区域为圆内的区域的面积，再利用积分知识可得正弦曲线y=sinx与x轴围成的区域记为M的面积为S=2∫0πsinxdx=-2cosx0π=4，代入几何概率的计算公式可
解答 解：构成试验的全部区域为圆内的区域，面积为16π，
正弦曲线y=sinx与x轴围成的区域记为M，面积为S=2∫0πsinxdx=-2cosx|0π=4
由几何概率的计算公式可得，随机往圆O内投一个点A，
则点A落在区域M外的概率P=1-$\frac{4}{16π}$=1-$\frac{1}{4π}$；
故答案为：$1-\frac{1}{4π}$．
点评 本题主要考查了利用积分求解曲面的面积，几何概率的计算公式的运用，属于中档试题，具有一定的综合性．
练习册系列答案
相关题目
14．已知集合M={x|-1≤x≤2}，N={x|1-3a＜x≤2a}，若M∩N=M，则实数a的取值范围是（ ）
| A． | （$\frac{2}{3}$，1） | B． | （1，+∞） | C． | （$\frac{2}{3}$，+∞） | D． | [1，+∞） |
1．（$\sqrt{x}$-$\frac{2}{x}$）8的展开式中，x的系数为（ ）
| A． | -112 | B． | 112 | C． | 56 | D． | -56 |
11．已知F是抛物线y2=4x的焦点，过点F且斜率为$\sqrt{3}$的直线交抛物线于A，B两点，则||FA|2-|FB|2|的值为（ ）
| A． | $\frac{28}{3}$ | B． | $\frac{128}{9}$ | C． | $\frac{128}{8}\sqrt{3}$ | D． | $\frac{28}{3}\sqrt{2}$ |