题目内容
1．
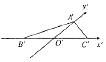如图，△A'B'C'是△ABC用“斜二测画法”画出的直观图，其中O'B'=O'C'=1，O'A'=$\frac{{\sqrt{3}}}{2}$，那么△ABC是一个（ ）| A． | 等边三角形 | B． | 直角三角形 | ||
| C． | 钝角三角形 | D． | 三边互不相等的三角形 |
分析 根据“斜二测画法”的画图法则，结合已知，可得△ABC中，BO=CO=1，AO=$\sqrt{3}$，结合勾股定理，求出△ABC的三边长，可得△ABC的形状．
解答 解：由已知中△ABC的直观图中O'B'=O'C'=1，O'A'=$\frac{{\sqrt{3}}}{2}$，
∴△ABC中，BO=CO=1，AO=$\sqrt{3}$，
由勾股定理得：AB=AC=2，
又由BC=2，
故△ABC为等边三角形，
故选：A．
点评 本题考查的知识点是斜二侧画几何体的直观图，三角形形状的判断，难度不大，属于基础题．
练习册系列答案
相关题目
11．已知复数z满足（1-i）z=i，则复数$\overline{z}$在复平面内的对应点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
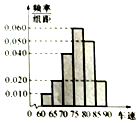交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速（单位：km/h），现将其分成六组为[60，65），[65，70），[70，75），[75，80），[80，85），[85，90]后得到如图所示的频率分布直方图．
13．“α=$\frac{π}{6}$”是$tan（{π-a}）=-\frac{{\sqrt{3}}}{3}$的（ ）
| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分又不必要条件 |
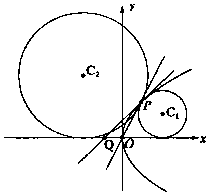如图所示，在直角坐标系xOy中，抛物线C：y2=4x，Q（-1，0），设点P是第一象限内抛物线C上一点，且PQ为抛物线C的切线．