题目内容
13．“α=$\frac{π}{6}$”是$tan（{π-a}）=-\frac{{\sqrt{3}}}{3}$的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充分必要条件 | D． | 既不充分又不必要条件 |
分析 根据充分必要条件的定义以及三角函数的性质判断即可．
解答 解：若“α=$\frac{π}{6}$”，则$tan（{π-a}）=-\frac{{\sqrt{3}}}{3}$，是充分条件，
反之，不成立，
故选：A．
点评 本题考查了充分必要条件，考查三角函数的性质，是一道基础题．
练习册系列答案
相关题目
3．设正项等差数列{an}的前n项和为Sn，若S2017=4034，则$\frac{1}{a_9}+\frac{9}{{{a_{2009}}}}$的最小值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{9}{4}$ | C． | 2 | D． | 4 |
4．已知a=$\frac{1}{6}$ln8，b=$\frac{1}{2}$ln5，c=ln$\sqrt{6}$-ln$\sqrt{2}$，则（ ）
| A． | a＜b＜c | B． | a＜c＜b | C． | c＜a＜b | D． | c＜b＜a |
1．
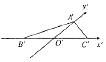如图，△A'B'C'是△ABC用“斜二测画法”画出的直观图，其中O'B'=O'C'=1，O'A'=$\frac{{\sqrt{3}}}{2}$，那么△ABC是一个（ ）
如图，△A'B'C'是△ABC用“斜二测画法”画出的直观图，其中O'B'=O'C'=1，O'A'=$\frac{{\sqrt{3}}}{2}$，那么△ABC是一个（ ）| A． | 等边三角形 | B． | 直角三角形 | ||
| C． | 钝角三角形 | D． | 三边互不相等的三角形 |
8．如图为某几何体的三视图，则该几何体的内切球的直径为（ ）
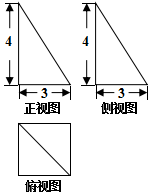
| A． | 2 | B． | 1 | C． | $\frac{1}{2}$ | D． | 4 |
2．用计算器演算函数y=f（x）=xx，x∈（0，1）的若干值，可以猜想下列命题中真命题只能是（ ）
| A． | y=f（x）在区间（0，0.4）上递减 | B． | y=f（x）在区间（0.35，1）上递减 | ||
| C． | y=f（x）的最小值为f（0.4） | D． | y=f（x）在（0.3，0.4）上有最小值 |