题目内容
6.若函数f(x)=|2x-1|-m有两个不同的零点,则实数m的取值范围是(0,1).分析 把函数f(x)=|2x-1|-m的零点转化为函数y=|2x-1|与y=m的图象交点的横坐标,画出两个函数的图象,数形结合得答案.
解答 解:由f(x)=|2x-1|-m=0,得|2x-1|=m,
画出函数y=|2x-1|与y=m的图象如图,
由图可知,要使函数f(x)=|2x-1|-m有两个不同的零点,则实数m的取值范围是(0,1).
故答案为:(0,1).
点评 本题考查函数的零点判定定理,考查了数学转化思想方法和数形结合的解题思想方法,是中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
17.log525=( )
| A. | 5 | B. | 2 | C. | 3 | D. | 4 |
14.若抛物线x2=ay的焦点为F(0,2),则a的值为( )
| A. | $\frac{1}{4}$ | B. | 4 | C. | $\frac{1}{8}$ | D. | 8 |
1.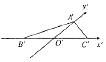 如图,△A'B'C'是△ABC用“斜二测画法”画出的直观图,其中O'B'=O'C'=1,O'A'=$\frac{{\sqrt{3}}}{2}$,那么△ABC是一个( )
如图,△A'B'C'是△ABC用“斜二测画法”画出的直观图,其中O'B'=O'C'=1,O'A'=$\frac{{\sqrt{3}}}{2}$,那么△ABC是一个( )
 如图,△A'B'C'是△ABC用“斜二测画法”画出的直观图,其中O'B'=O'C'=1,O'A'=$\frac{{\sqrt{3}}}{2}$,那么△ABC是一个( )
如图,△A'B'C'是△ABC用“斜二测画法”画出的直观图,其中O'B'=O'C'=1,O'A'=$\frac{{\sqrt{3}}}{2}$,那么△ABC是一个( )| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 三边互不相等的三角形 |
11.已知集合M={x|(x+3)(x-1)≤0},N={x|log2x≤1},则M∪N=( )
| A. | [-3,2] | B. | [-3,2) | C. | [1,2] | D. | (0,2] |
15.衡州中学有教师150人,其中高级教师15人,中级教师90人,现按职称分层抽样选出30名教师参加教职工代表大会,则选出的高、中、初级教师的人数分别为( )
| A. | 5,10,15 | B. | 3,18,9 | C. | 3,10,17 | D. | 5,9,16 |