题目内容
1.已知二次函数f(x)=3x2-2x,数列{an}的前n项和为Sn,点$(n,{S_n})\;(n∈{N^*})$均在函数y=f(x)的图象上.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设${b_n}=\frac{3}{{{a_n}{a_{n+1}}}},{T_n}$是数列{bn}的前n项和,求使得${T_n}<\frac{m}{2014}$对所有的n∈N*都成立的最小正整数m.
分析 (Ⅰ)根据点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,确定出Sn,由an=Sn-Sn-1确定出通项公式即可;
(Ⅱ)由第一问确定出的通项公式表示出bn,进而表示出Tn,代入已知不等式确定出最小正整数m的值即可.
解答 解:(Ⅰ)∵f(x)=3x2-2x,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上,
∴Sn=3n2-2n,
当n≥2时,an=Sn-Sn-1=3n2-2n-[3(n-1)2-2(n-)]=6n-5,
当n=1时a1=1也适合,
∴an=6n-5(n∈N*);
(Ⅱ)由(Ⅰ)知bn=$\frac{3}{{a}_{n}{a}_{n+1}}$=$\frac{3}{(6n-5)[6(n+1)-5]}$=$\frac{1}{2}$($\frac{1}{6n-5}$-$\frac{1}{6n+1}$),
∴Tn=$\frac{1}{2}$[(1-$\frac{1}{7}$)+($\frac{1}{7}$-$\frac{1}{13}$)+…+($\frac{1}{6n-5}$-$\frac{1}{6n+1}$)]=$\frac{1}{2}$(1-$\frac{1}{6n+1}$),
要使$\frac{1}{2}$(1-$\frac{1}{6n+1}$)<$\frac{m}{2014}$(n∈N*)成立,m必须且仅需满足$\frac{1}{2}$≤$\frac{m}{2014}$,即m≥1007,
则满足要求的最小正整数m为1007.
点评 此题考查了数列的递推式,二次函数的性质,熟练掌握运算法则及性质是解本题的关键.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
12.现有四个函数:①y=x•sinx;②y=x•cosx;③y=x•|cosx|;④y=x•2x的图象(部分)如图,则按照从左到右的顺序,图象对应的函数序号正确的一组是( )
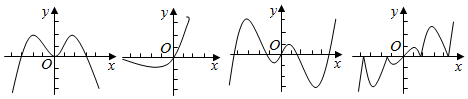
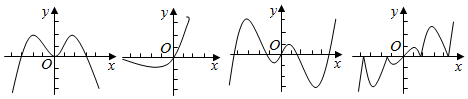
| A. | ①④③② | B. | ①④②③ | C. | ④①②③ | D. | ③④②① |
16.在△ABC中,BC=1,ccosA+acosC=2bcosB,△ABC的面积S=$\sqrt{3}$,则AC等于( )
| A. | $\sqrt{13}$ | B. | 4 | C. | 3 | D. | $\sqrt{15}$ |
13.若A(xl,y1),B(x2,y2)为平面上两点,则定义A?B=x1y1+x2y2,已知点M($\sqrt{3}$,sinx),N(-1,cosx),设函数f(x)=M?N,将f(x)的图象向左平移φ(φ>0)个单位长度后,所得图象关于y轴对称,则φ的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
10.下列各式中正确的是( )
| A. | sin(arcsin$\frac{π}{3}$)=$\frac{π}{3}$ | B. | sin(arcsin$\frac{3}{π}$)=$\frac{3}{π}$ | ||
| C. | arccos(-x)=arccosx | D. | arctan(tan$\frac{2π}{3}$)=$\frac{2π}{3}$ |
7.已知数列{an}是等差数列,数列{bn}是等比数列,公比为q,数列{cn}中,cn=anbn,Sn是数列{cn}前n项和,若Sm=11,S2m=7,S3m=-201(m为正偶数),则S4m的值为( )
| A. | -1601 | B. | -1801 | C. | -2001 | D. | -2201 |