题目内容
已知圆C的圆心在y轴负半轴上,半径为3,且直线y+1=0与圆C相切,
(1)求圆C的方程;
(2)若圆C与直线x-y-1=0交于A、B两点,求A、B两点间的距离|AB|.
(1)求圆C的方程;
(2)若圆C与直线x-y-1=0交于A、B两点,求A、B两点间的距离|AB|.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(1)设出圆的方程,利用直线y+1=0与圆C相切,可求圆C的方程;
(2)求出圆C与直线x-y-1=0的交点坐标,利用两点间的距离公式,求出|AB|.
(2)求出圆C与直线x-y-1=0的交点坐标,利用两点间的距离公式,求出|AB|.
解答:
解:(1)设圆C的方程:x2+(y-b)2=9(b<0),
∵直线y+1=0与圆C相切,
∴|b-(-1)|=3,
∵b<0,
∴b=-4,
∴圆C的方程:x2+(y+4)2=9;
(2)由
,可得
或
,
∴|AB|=
=3
.
∵直线y+1=0与圆C相切,
∴|b-(-1)|=3,
∵b<0,
∴b=-4,
∴圆C的方程:x2+(y+4)2=9;
(2)由
|
|
|
∴|AB|=
| (0+3)2+(-1+4)2 |
| 2 |
点评:本题考查圆的方程,考查直线与圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
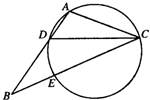 如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC
如图,在△ABC中,CD是∠ACB的角平分线,△ADC的外接圆交BC于点E,AB=2AC 如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有
如图所示,用五种不同的颜色分别给A,B,C,D四个区域涂色,相邻区域必须涂不同颜色,若允许同一种颜色多次使用,则不同的涂色方法共有