题目内容
已知函数f(x)=2x,等差数列{an}的公差为2,a1=1,则log2[f(a1)•f(a2)…f(a10)]= .
考点:等差数列的性质
专题:等差数列与等比数列
分析:利用等差数列的前n项和公式、指数函数和对数函数的运算性质即可得出.
解答:
解:∵等差数列{an}的公差为2,a1=1,
∴S10=10×1+
×2=100,
∴f(a1)•f(a2)…f(a10)=2a1•2a2…•2a10=2a1+a2+…+a10=2S10=2100.
∴log2[f(a1)•f(a2)…f(a10)]=log22100=100.
故答案为:100.
∴S10=10×1+
| 10×9 |
| 2 |
∴f(a1)•f(a2)…f(a10)=2a1•2a2…•2a10=2a1+a2+…+a10=2S10=2100.
∴log2[f(a1)•f(a2)…f(a10)]=log22100=100.
故答案为:100.
点评:本题考查了等差数列的前n项和公式、指数函数和对数函数的运算性质,属于中档题.

练习册系列答案
相关题目
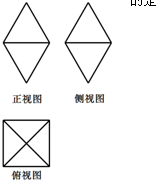 如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为
如图是某宝石饰物的三视图,已知该饰物的正视图、侧视图都是面积为