题目内容
已知向量
=（cosx，-sinx），
=（cosx，sinx-2
cosx），x∈R，令f（x）=
•
，
（1）求函数f（x）的单调递增区间；
（2）当x∈[0，
]时，求函数f（x）的值域．
| m |
| n |
| 3 |
| m |
| n |
（1）求函数f（x）的单调递增区间；
（2）当x∈[0，
| π |
| 4 |
考点：三角函数中的恒等变换应用,平面向量数量积的运算
专题：三角函数的图像与性质
分析：（1）利用倍角公式和两角和公式对函数解析式化简整理后，利用了三角函数图象和性质求得其单调区间．
（2）根据x的范围，利用三角函数图象和性质求得函数的在此范围上最大和最小值，得到函数在[0，
]的值域．
（2）根据x的范围，利用三角函数图象和性质求得函数的在此范围上最大和最小值，得到函数在[0，
| π |
| 4 |
解答：
解：（1）f（x）=
•
=cos2x-sinx(sinx-2
cosx)=cos2x+
sin2x=2sin(2x+
)，
∵函数y=sinx的单调增区间为[2kπ-
，2kπ+
]，k∈Z
∴2kπ-
≤2x+
≤2kπ+
，
∴kπ-
≤x≤kπ+
，k∈Z
∴函数f（x）的单调递增区间为[kπ-
，kπ+
]，k∈Z
（2）当x∈[0，
]时，
≤2x+
≤
，
∴1≤2sin(2x+
)≤2
∴函数f（x）的值域为[1，2]．
| m |
| n |
| 3 |
| 3 |
| π |
| 6 |
∵函数y=sinx的单调增区间为[2kπ-
| π |
| 2 |
| π |
| 2 |
∴2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
∴kπ-
| π |
| 3 |
| π |
| 6 |
∴函数f（x）的单调递增区间为[kπ-
| π |
| 3 |
| π |
| 6 |
（2）当x∈[0，
| π |
| 4 |
| π |
| 6 |
| π |
| 6 |
| 2π |
| 3 |
∴1≤2sin(2x+
| π |
| 6 |
∴函数f（x）的值域为[1，2]．
点评：本题主要考查了三角函数恒等变换的应用，三角函数图象和性质．要求对三角函数的图象能熟练记忆，利用图象来解决三角函数的问题．
练习册系列答案
相关题目
如图所示的茎叶图记录了甲、乙两个小组（每小组4人）在期末考试中的数学成绩．乙组记录中有一个数据模糊，无法确认，在图中以a表示．已知甲、乙两个小组的数学成绩的平均分相同．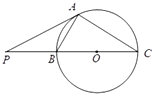
如图，PA是圆O的切线，切点为A，PO交圆O于B，C两点，PA=