题目内容
已知函数f(x)=x3+ax2+bx+c在x=-
与x=1时都取得极值
(1)求a,b的值与函数f(x)的单调区间
(2)若f(0)=1,且对x∈[-1,2],不等式f(x)<m+1恒成立,求m的取值范围.
| 2 |
| 3 |
(1)求a,b的值与函数f(x)的单调区间
(2)若f(0)=1,且对x∈[-1,2],不等式f(x)<m+1恒成立,求m的取值范围.
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:导数的综合应用
分析:(1)f′(x)=3x2+2ax+b,由于函数f(x)在x=-
与x=1时都取得极值,可得f′(-
)=f′(1)=0,解出即可得出a,b.列出表格即可得出单调性极值.
(2)对x∈[-1,2],不等式f(x)<m+1恒成立?f(x)max<m+1,利用(1)的单调性极值与最值即可得出.
| 2 |
| 3 |
| 2 |
| 3 |
(2)对x∈[-1,2],不等式f(x)<m+1恒成立?f(x)max<m+1,利用(1)的单调性极值与最值即可得出.
解答:
解:(1)函数f(x)=x3+ax2+bx+c,f′(x)=3x2+2ax+b,
∵函数f(x)在x=-
与x=1时都取得极值,
∴f′(-
)=f′(1)=0,
∴
,
解得a=-
,b=-2.
∴f′(x)=3(x+
)(x-1),
当x变化时,f′(x),f(x)变化如下表:
∴函数f(x)的递增区间是(-∞,-
),(1,+∞),递减区间是(-
,1);
(2)f(0)=1,∴c=1.∴f(x)=x3-
x2-2x+1,x∈[-1,2].
当x=-
时,f(-
)=
为极大值.而f(2)=3,则f(2)=3为最大值,
要使f(x)<m+1恒成立,则只需要3<m+1,
解得m>2,
∴实数m的取值范围为m>2.
∵函数f(x)在x=-
| 2 |
| 3 |
∴f′(-
| 2 |
| 3 |
∴
|
解得a=-
| 1 |
| 2 |
∴f′(x)=3(x+
| 2 |
| 3 |
当x变化时,f′(x),f(x)变化如下表:
x | (-∞,-
| -
| (-
| 1 | (1,+∞) | ||||||
| f′(x) | + | 0 | - | 0 | + | ||||||
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
| 2 |
| 3 |
| 2 |
| 3 |
(2)f(0)=1,∴c=1.∴f(x)=x3-
| 1 |
| 2 |
当x=-
| 2 |
| 3 |
| 2 |
| 3 |
| 49 |
| 27 |
要使f(x)<m+1恒成立,则只需要3<m+1,
解得m>2,
∴实数m的取值范围为m>2.
点评:本题考查了利用导数研究函数的单调性极值与最值、闭区间上的最值,考查了分析问题与解决问题的能力,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
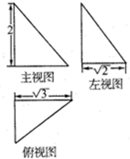
已知某几何体的三视图如图所示,则该几何体的体积是( )


A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
沿一个正方体三个面的对角线截得几何体如图所示,则该几何体的侧视图为( )


A、 |
B、 |
C、 |
D、 |
若某空间几何体的三视图如右图所示,则该几何体的体积是( )


| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
若
•
=-9,|
|=3,<
,
>=
,则|
|=( )
| a |
| b |
| a |
| a |
| b |
| 2π |
| 3 |
| b |
| A、3 | B、6 | C、9 | D、12 |