题目内容
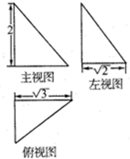
已知某几何体的三视图如图所示,则该几何体的外接球的表面积为 .

考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥,求出其外接球的半径,代入表面积公式,可得答案.
解答:
解:由已知的三视图可得:该几何体是一个以俯视图为底面的三棱锥,
其四个顶点是以俯视图为底面,以2为高的三棱柱的四个顶点,
故其外接球,即为以俯视图为底面,以2为高的三棱柱的外接球,
由底面两直角边长分别为
,
,
故底面的外接圆直径为
,故底面的外接圆半径r=
,
球心距d=
h=1,
故球的半径R=
=
,
故该几何体的外接球的表面积S=4πR2=9π,
故答案为:9π.
其四个顶点是以俯视图为底面,以2为高的三棱柱的四个顶点,
故其外接球,即为以俯视图为底面,以2为高的三棱柱的外接球,
由底面两直角边长分别为
| 2 |
| 3 |
故底面的外接圆直径为
| 5 |
| ||
| 2 |
球心距d=
| 1 |
| 2 |
故球的半径R=
| r2+d2 |
| 3 |
| 2 |
故该几何体的外接球的表面积S=4πR2=9π,
故答案为:9π.
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
下列选项叙述错误的是( )
| A、命题“若x≠0,则ex≠1”的逆否命题是“若ex=1,则x=0” | ||
B、“x>2”是“
| ||
| C、若命题p:?x∈R,x2+x+1>0,则¬p:?x0∈R,使得x02+x0+1≤0 | ||
| D、若p∧q为假命题,则p,q均为假命题 |
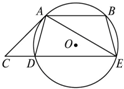 如图,四边形ABED内接于⊙O,AB∥DE,AC切⊙O于A,交ED延长线于C.若AD=BE=
如图,四边形ABED内接于⊙O,AB∥DE,AC切⊙O于A,交ED延长线于C.若AD=BE=