题目内容
在△ABC中，若c=2bcosA，则此三角形必是 ．
考点：余弦定理
专题：解三角形
分析：已知等式利用正弦定理化简，把sinC=sin（A+B）代入，利用两角和与差的正弦函数公式化简，整理得到A=B，即可确定出三角形形状．
解答：
解：由c=2bcosA，利用正弦定理化简得：sinC=2sinBcosA，
把sin（A+B）=sinAcosB+cosAsinB代入得：sinAcosB+cosAsinB=2sinBcosA，
即sinAcosB-cosAsinB=sin（A-B）=0，即A-B=0，
∴A=B，即a=b，
则△ABC为等腰三角形，
故答案为：等腰三角形
把sin（A+B）=sinAcosB+cosAsinB代入得：sinAcosB+cosAsinB=2sinBcosA，
即sinAcosB-cosAsinB=sin（A-B）=0，即A-B=0，
∴A=B，即a=b，
则△ABC为等腰三角形，
故答案为：等腰三角形
点评：此题考查了正弦定理，以及两角和与差的正弦函数公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
相关题目
已知a=
，b=20.8，c=2log52，则a，b，c的大小关系为（ ）
| 2 |
| A、c＜b＜a |
| B、b＜c＜a |
| C、b＜a＜c |
| D、c＜a＜b |
已知集合M={-1，1，2}，N={x∈R|x2-5x+4=0}，则M∪N=（ ）
| A、ϕ | B、{1} |
| C、{1，4} | D、{-1，1，2，4} |
在区间[0，2π]上任取一个数x，则使得2sinx＞1的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
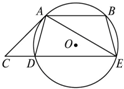如图，四边形ABED内接于⊙O，AB∥DE，AC切⊙O于A，交ED延长线于C．若AD=BE=