题目内容
若某空间几何体的三视图如右图所示,则该几何体的体积是( )


| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由已知的三视图可得:该几何体是一个以左视图为底面的三棱柱,计算出底面面积和高,代入棱柱体积公式,可得答案.
解答:
解:由已知的三视图可得:该几何体是一个以左视图为底面的三棱锥,
棱柱的底面面积S=
×
×1=
,
棱柱的高h=
,
故棱柱的体积V=Sh=1,
故选:A
棱柱的底面面积S=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
棱柱的高h=
| 2 |
故棱柱的体积V=Sh=1,
故选:A
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在区间[0,2π]上任取一个数x,则使得2sinx>1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
“所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数”,上述推理( )
| A、推理形式不正确 |
| B、大前提错误 |
| C、错误,因为大小前提不一致 |
| D、完全正确 |
函数y=(ex-e-x)sinx的图象(部分)大致是( )
A、 |
B、 |
C、 |
D、 |
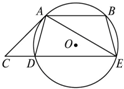 如图,四边形ABED内接于⊙O,AB∥DE,AC切⊙O于A,交ED延长线于C.若AD=BE=
如图,四边形ABED内接于⊙O,AB∥DE,AC切⊙O于A,交ED延长线于C.若AD=BE=