题目内容

3．已知如下等式：2+4=6；8+10+12=14+16；18+20+22+24=26+28+30；…以此类推，则2018会出现在第（　　）个等式中．
A．33B．30C．31D．32

分析 从已知等式分析，发现规律为：各等式首项分别为2×1，2（1+3），2（1+3+5），…，即可得出结论．

解答 解：①2+4=6；  
②8+10+12=14+16；
③18+20+22+24=26+28+30，…
其规律为：各等式首项分别为2×1，2（1+3），2（1+3+5），…，
所以第n个等式的首项为2[1+3+…+（2n-1）]=2×$\frac{n（1+2n-1）}{2}$=2n2，
当n=31时，等式的首项为2×312=1932，
当n=32时，等式的首项为2×322=2048，
所以2018在第31个等式中，
故选：C．

点评 本题考查归纳推理，难点是根据能够找出数之间的内在规律，考查观察、分析、归纳的能力，是基础题．

练习册系列答案
相关题目
13．已知$f（{2^x}）=\frac{1}{x}$，则f（3）=（　　）
A．$\frac{1}{3}$B．$\frac{1}{8}$C．log32D．log23
14．直线$\left\{{\begin{array}{l}{x=3+tcos{{230}°}\;\;}\\{y=-1+tsin{{230}°}}\end{array}}\right.$（t为参数）的倾斜角是（　　）
A．30°B．45°C．50°D．60°
11．德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数f（x）=$\left\{\begin{array}{l}1，x为有理数\\ 0，x为无理数\end{array}$，称为狄利克雷函数，则关于函数f（x）有以下四个命题：
①f（f（x））=1；
②函数f（x）是偶函数；
③任意一个非零有理数T，f（x+T）=f（x）对任意x∈R恒成立；
④存在三个点A（x1，f（x1）），B（x2，f（x2）），C（x3，f（x3）），使得△ABC为等边三角形．
其中真命题的个数是（　　）
A．4B．3C．2D．1
18．中国人口已经出现老龄化与少子化并存的结构特征，测算显示中国是世界上人口老龄化速度最快的国家之一，再不实施“放开二胎”新政策，整个社会将会出现一系列的问题，若某地区2015年人口总数为45万，实施“放开二胎”新政策后专家估计人口总数将发生如下变化：从2016年开始到2025年每年人口比上年增加0.5万人，从2026年开始到2035年每年人口为上一年的99%．
（1）求实施新政策后，从2016年开始到2035年，第n年的人口总数an的表达式；
（2）若新政策实施后的2016年到2035年人口平均值超过49万，则需调整政策，否则继续实施，问到2035年后是否需要调整政策？（说明：0.9910=（1-001）10≈0.9）．
8．已知边长为2$\sqrt{3}$的菱形ABCD中，∠A=60°，现沿对角线BD折起，使得AC=3$\sqrt{3}$，此时点A，B，C，D在同一个球面上，则该球的表面积为（　　）
A．20πB．24πC．28πD．32π
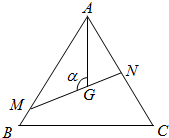6．如图，是△ABC边长为1的正三角形，M，N分别是AB，AC边上的点，线段MN过△ABC的重心，设∠MGA=α，$\frac{π}{3}$≤α≤$\frac{2π}{3}$．
（Ⅰ）当α=$\frac{2π}{3}$时，求MG的长；
（Ⅱ）分别记△AGM，△AGN的面积为S1，S2，试将S1，S2表示为α的函数；
（Ⅲ）设y=$\frac{1}{{{S}_{1}}^{2}}$+$\frac{1}{{{S}_{2}}^{2}}$，求y的最小值．
3．在△ABC中，a=$\sqrt{3}$b，A=120°，则B的大小为（　　）
A．30°B．45°C．60°D．90°
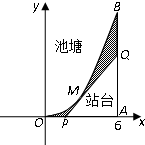4．如图，池塘的边缘为曲线段OMB，它可以近似看成是函数f（x）=x2在0≤x≤6的图象，BA垂直于x轴于点A，现要建一个以A为直角的观光站台△APQ，其中斜边PQ与曲线段OMB相切于点M（t，t2），切线PQ交x轴于点P，交线段AB于点Q，图中的阴影部分种植草坪．
（1）将△QAP的面积表达为t的函数；
（2）求草坪的面积的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网