题目内容
9.已知圆C与圆D:(x-1)2+(y+2)2=4关于直线y=x对称.(Ⅰ) 求圆C的标准方程;
(Ⅱ)若直线l:y=kx+1与圆C交于A、B两点,且|AB|=2$\sqrt{3}$,求直线l的方程.
分析 (Ⅰ)求出圆D:(x-1)2+(y+2)2=4的圆心为点D(1,-2),半径为2,因此所求圆的圆心为点D关于x=y对称点,圆半径为2,由此结合圆的标准方程即可得到所求圆的方程.
(Ⅱ)求出圆心C(-2,1)到直线l的距离d,由此利用勾股定理能求出k,从而能求出直线l的方程.
解答 解:(Ⅰ)圆D:(x-1)2+(y+2)2=4的圆心为点C(1,-2),半径r=2,
∵圆C与圆D:(x-1)2+(y+2)2=4关于直线y=x对称,
∴圆C的半径r=2,且圆心C为点D(1,-2)关于x=y对称点,即C(-2,1),
∴圆C的标准方程为:(x+2)2+(y-1)2=4.
(Ⅱ)∵直线l:y=kx+1与圆C交于A、B两点,且|AB|=2$\sqrt{3}$,
∴圆心C(-2,1)到直线l的距离为:
d=$\frac{|-2k-1+1|}{\sqrt{{k}^{2}+1}}$=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$,
且$(\sqrt{3})^{2}+(\frac{|2k|}{\sqrt{{k}^{2}+1}})^{2}$=4,
解得k=$±\frac{\sqrt{3}}{3}$,
∴直线l的方程为y=-$\frac{\sqrt{3}}{3}x+1$或y=$\frac{\sqrt{3}}{3}x+1$.
点评 本题考查圆的标准方程的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意圆的性质、直线方程的性质的合理运用.

练习册系列答案
相关题目
8.已知边长为2$\sqrt{3}$的菱形ABCD中,∠A=60°,现沿对角线BD折起,使得AC=3$\sqrt{3}$,此时点A,B,C,D在同一个球面上,则该球的表面积为( )
| A. | 20π | B. | 24π | C. | 28π | D. | 32π |
20.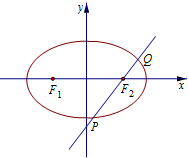 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )
 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1,(a>b>0),F1,F2分别为椭圆的左,右焦点,如图过F2且斜率为1的直线与椭圆相交于P,Q两点,且$\frac{{|P{F_2}|}}{{|Q{F_2}|}}$=2,则椭圆的离心率e=( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
14.函数y=x3-3x2-9x(0<x<4)有( )
| A. | 极大值5,极小值-27 | B. | 极大值5,极小值-11 | ||
| C. | 极大值5,无极小值 | D. | 极小值-27,无极大值 |
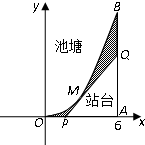 如图,池塘的边缘为曲线段OMB,它可以近似看成是函数f(x)=x2在0≤x≤6的图象,BA垂直于x轴于点A,现要建一个以A为直角的观光站台△APQ,其中斜边PQ与曲线段OMB相切于点M(t,t2),切线PQ交x轴于点P,交线段AB于点Q,图中的阴影部分种植草坪.
如图,池塘的边缘为曲线段OMB,它可以近似看成是函数f(x)=x2在0≤x≤6的图象,BA垂直于x轴于点A,现要建一个以A为直角的观光站台△APQ,其中斜边PQ与曲线段OMB相切于点M(t,t2),切线PQ交x轴于点P,交线段AB于点Q,图中的阴影部分种植草坪. 如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.
如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,∠BAC=90°,F为棱AA1上的动点,A1A=4,AB=AC=2.