若函数f(x)=x2+x-lnx+1在其定义域的一个子区间内不是单调函数.则实数k的取值范围是( )A．(-$\frac{3}{2}$.$\frac{3}{4}$)B．[$\frac{1}{2}$.3)C．D．[$\frac{1}{2}$.$\frac{3}{4}$) 题目和参考答案——青夏教育精英家教网—

题目内容

19．若函数f（x）=x²+x-lnx+1在其定义域的一个子区间（2k-1，k+2）内不是单调函数，则实数k的取值范围是（　　）

A．

（-$\frac{3}{2}$，$\frac{3}{4}$）

B．

[$\frac{1}{2}$，3）

C．

（-$\frac{3}{2}$，3）

D．

[$\frac{1}{2}$，$\frac{3}{4}$）

分析先求出函数的导数，令导函数为0，求出x的值，得到不等式解出k的值即可．

解答解：函数的定义域为（0，+∞），所以2k-1≥0即k≥$\frac{1}{2}$，
f′（x）=2x+1-$\frac{1}{x}$=$\frac{（x+1）（2x-1）}{x}$，令f′（x）=0，得x=$\frac{1}{2}$或x=-1（不在定义域内舍），
由于函数在区间（2k-1，k+2）内不是单调函数，所以$\frac{1}{2}$∈（2k-1，k+2），
即2k-1＜$\frac{1}{2}$＜k+2，解得：-$\frac{3}{2}$＜k＜$\frac{3}{4}$，
综上得$\frac{1}{2}$≤k＜$\frac{3}{4}$，
故选：D．

点评本题考查了函数的单调性，导数的应用，是一道基础题．

练习册系列答案

10．长方体ABCD-A₁B₁C₁D₁中，AB=1，BC=2，AA₁=3，点M是BC中点，点P∈AC₁，Q∈MD，则|PQ|长度最小值为$\frac{{2\sqrt{3}}}{3}$．

7．各项均为正数的数列{a_n}中，前n项和${S_n}={（{\frac{{{a_n}+1}}{2}}）^2}$．
（1）求数列{a_n}的通项公式；
（2）若$\frac{1}{{{a_1}{a_2}}}+\frac{1}{{{a_2}{a_3}}}+…+\frac{1}{{{a_n}{a_{n+1}}}}$＜k恒成立，求k的取值范围；
（3）是否存在正整数m，k，使得a_m，a_m+5，a_k成等比数列？若存在，求出m和k的值，若不存在，请说明理由．

14．已知函数f（x）=$\sqrt{2}$（sin2ωxcos$\frac{π}{4}$+cos2ωx•sin$\frac{π}{4}$）（ω＞0），且f（x）的最小正周期为π．
（1）求函数f（x）的单调增区间；
（2）若f（$\frac{α}{2}$-$\frac{π}{8}$）=$\frac{\sqrt{2}}{3}$，f（$\frac{β}{2}$-$\frac{π}{8}$）=$\frac{2\sqrt{2}}{3}$，且α、β∈（-$\frac{π}{2}$，$\frac{π}{2}$），求cos（α+β）的值．

4．

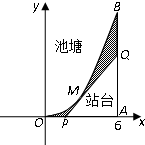如图，池塘的边缘为曲线段OMB，它可以近似看成是函数f（x）=x²在0≤x≤6的图象，BA垂直于x轴于点A，现要建一个以A为直角的观光站台△APQ，其中斜边PQ与曲线段OMB相切于点M（t，t²），切线PQ交x轴于点P，交线段AB于点Q，图中的阴影部分种植草坪．
（1）将△QAP的面积表达为t的函数；
（2）求草坪的面积的最小值．

11．已知函数f（x）=sin（x+$\frac{7π}{4}$）+cos（x-$\frac{3π}{4}$），x∈R．
（1）求f（x）的最小正周期和最小值；
（2）已知f（α）=$\frac{6}{5}$，0＜α＜$\frac{3π}{4}$，求f（2α）的值．

8．关于函数f（x）=log${\;}_{\frac{1}{2}}$（1-2x）的单调性，叙述正确的是（　　）

	A．	f（x）在（$\frac{1}{2}$，+∞）内是增函数		B．	f（x）在（$\frac{1}{2}$，+∞）内是减函数
	C．	f（x）在（-∞，$\frac{1}{2}$）内是增函数		D．	f（x）在（-∞，$\frac{1}{2}$）内是减函数

9．设函数f（x）=2cos（$\frac{x}{2}$-$\frac{π}{3}$）+1
（1）求f（x）的最小正周期；对称轴方程和对称中心的坐标
（2）求f（x）在区间[0，2π]的最大值和最小值．

试题分类