题目内容
19.若函数y=f(x)(x∈R)满足f(x-2)=f(x),且x∈[-1,1],f(x)=1-x2,函数g(x)=$\left\{\begin{array}{l}{lgx(x>0)}\\{-\frac{1}{x}(x<0)}\end{array}\right.$则函数h(x)=f(x)-g(x)在区间[-4,5]内零点的个数为( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 由函数y=f(x)(x∈R)满足f(x-2)=f(x),可知函数y=f(x)(x∈R)是周期为2的函数,进而根据x∈[-1,1]时,f(x)=1-x2,函数g(x)=$\left\{\begin{array}{l}{lgx(x>0)}\\{-\frac{1}{x}(x<0)}\end{array}\right.$的图象得到交点个数.
解答 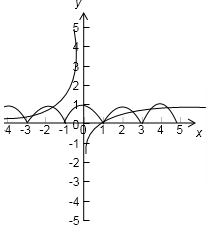 解:因为f(x-2)=f(x),所以函数y=f(x)(x∈R)是周期为2函数.
解:因为f(x-2)=f(x),所以函数y=f(x)(x∈R)是周期为2函数.
因为x∈[-1,1]时,f(x)=1-x2,所以作出它的图象,
利用函数y=f(x)(x∈R)是周期为2函数,可作出y=f(x)在区间[-4,5]上的图象,如图所示
再作出函数g(x)=$\left\{\begin{array}{l}{lgx(x>0)}\\{-\frac{1}{x}(x<0)}\end{array}\right.$的图象,
容易得出到交点为7个.
故选:B.
点评 本题的考点是函数零点与方程根的关系,主要考查函数零点的定义,关键是正确作出函数图象,注意掌握周期函数的一些常见结论:若f(x+a)=f(x),则周期为a;若f(x+a)=-f(x),则周期为2a;若f(x+a)=$\frac{1}{f(x)}$,则周期为2a.

练习册系列答案
相关题目
10.已知a∈R,则“a>3”是“a2>2a+3”成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
8.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0\;\;,\;\;b>0})$的一个焦点为(5,0),渐近线方程为$y=±\frac{3}{4}x$,则该双曲线的方程为( )
| A. | $\frac{x^2}{16}-\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | C. | $\frac{x^2}{4}-\frac{y^2}{3}=1$ | D. | $\frac{x^2}{3}-\frac{y^2}{4}=1$ |
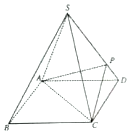 如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.
如图所示,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,点P在侧棱SD上,且SP=3PD.