题目内容
2.化简:已知α是第四象限角,则$cosα\sqrt{\frac{1-sinα}{1+sinα}}+sinα\sqrt{\frac{1-cosα}{1+cosα}}$=cosα-sinα.分析 根据同角三角函数关系式以及角象限符号的判断化简即可.
解答 解:由$cosα\sqrt{\frac{1-sinα}{1+sinα}}+sinα\sqrt{\frac{1-cosα}{1+cosα}}$=cosα$\sqrt{\frac{(1-sinα)^{2}}{1-si{n}^{2}α}}$+sinα$\sqrt{\frac{(1-cosα)^{2}}{1-co{s}^{2}α}}$=cosα$•\frac{1-sinα}{|cosα|}$+$\frac{1-cosα}{|sinα|}$,
∵α是第四象限角,
∴|cosα|=cosα,|sinα|=-sinα,
故得$cosα\sqrt{\frac{1-sinα}{1+sinα}}+sinα\sqrt{\frac{1-cosα}{1+cosα}}$=cosα-sinα,
故答案为:cosα-sinα,
点评 本题主要考查了同角三角函数关系式以及角象限符号的判断,属于基础知识的考查.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
20.若函数f(x)=2sin(2x+φ)(|φ|<$\frac{π}{2}$)的图象向右平移$\frac{π}{6}$个单位后经过点($\frac{π}{12}$,-$\sqrt{2}$),则φ等于( )
| A. | -$\frac{π}{12}$ | B. | -$\frac{π}{6}$ | C. | 0 | D. | $\frac{π}{6}$ |
17.设a,b,c∈R,且a>b,则下列选项中一定成立的是( )
| A. | ac>bc | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | a2>b2 | D. | a3>b3 |
7.设函数f(x)=$\left\{\begin{array}{l}{2sinx,0≤x≤π}\\{{x}^{2},x<0}\end{array}\right.$,则函数y=f(f(x))-1的零点的个数是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 无数个 |
12.已知向量$\overrightarrow a=({1-t\;\;,\;\;2t-1\;\;,\;\;0})$,$\overrightarrow b=({2\;\;,\;\;t\;\;,\;\;t})$(t∈R),则$|{\overrightarrow b-\overrightarrow a}|$的最小值是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
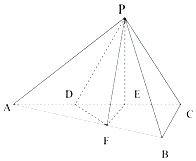 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.