题目内容
7.已知函数f(x)=x+alnx(a∈R),g(x)=ex-1(1)若直线y=0与函数y=f(x)的图象相切,求a的值;
(2)设a>0,对于?x1,x2∈[3,+∞)(x1≠x2)都有|f(x1)-f(x2)|<|g(x1)-g(x2)|,求实数a的取值范围.
分析 (1)求出函数的导数,设出切点坐标,求出a的值即可;
(2)根据函数的单调性,问题转化为f(x1)-g(x1)>f(x2)-g(x2),设h(x)=f(x)-g(x),根据函数的单调性求出a的范围即可.
解答 解:(1)f′(x)=1+$\frac{a}{x}$,设切点为(x0,0),
得1+$\frac{a}{{x}_{0}}$=0得x0=-a,
所以-a+aln(-a)=0,
所以a=-e;
(2)∵a>0∴x∈[3,+∞)时,f′(x)>0,
所以f(x),g(x)在x∈[3,+∞)上为增函数,
不妨设x1<x2,则f(x1)<f(x2),g(x1)<g(x2),
所以|f(x1)-f(x2)|<|g(x1)-g(x2)|,
可化为f(x2)-f(x1)<g(x2)-g(x1),
即f(x1)-g(x1)>f(x2)-g(x2),
设h(x)=f(x)-g(x),
则h(x)在x∈[3,+∞)递减,
h′(x)=1+$\frac{a}{x}$-ex≤0在x∈[3,+∞)恒成立,
即xex-x≥a在x∈[3,+∞)恒成立,
设v(x)=xex-x,
则∵x∈[3,+∞)∴v'(x)=ex+xex-1>0,
所以v(x)=xex-x在x∈[3,+∞)上为增函数
所以$v{(x)_{min}}=3{e^3}-3$,
∴a≤3e3-3.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,绝对值问题,是一道中档题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
2.若$a={2^x},b={log_{\frac{1}{2}}}x$则“x>1”是“a>b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.△ABC中,c是a与b的等差中项,sinA,sinB,sinC依次为一等比数列的前n项,前2n项,前3n项的和,则cosC的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
1.设{an}是等差数列,若a2=3,a9=7,则数列{an}前10项和为( )
| A. | 25 | B. | 50 | C. | 100 | D. | 200 |
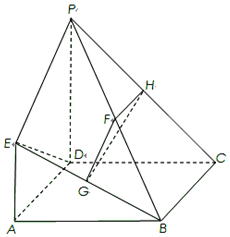 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.