题目内容
观察下列等式：
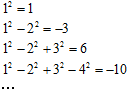
照此规律，第n个等式可为 ．
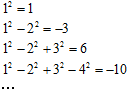
照此规律，第n个等式可为
考点：归纳推理
专题：推理和证明
分析：根据题中所给的规律，进行归纳猜想，得出本题结论．
解答：
解：由题意知：
12=1，
12-22=-（22-12）=-（2-1）（2+1）=-（1+2）=-3，
12-22+32=1+（32-22）=1+（3-2）（3+2）=1+2+3=6，
12-22+32-42=-（22-12）-（42-32）=-（1+2+3+4）=-10，
…
12-22+32-42+…+（-1）n+1n2=（-1）n+1（1+2+3+…+n）=（-1）n+1•
．
∴照此规律，第n个等式可为12-22+32-42+…+（-1）n+1n2=（-1）n+1•
．
12=1，
12-22=-（22-12）=-（2-1）（2+1）=-（1+2）=-3，
12-22+32=1+（32-22）=1+（3-2）（3+2）=1+2+3=6，
12-22+32-42=-（22-12）-（42-32）=-（1+2+3+4）=-10，
…
12-22+32-42+…+（-1）n+1n2=（-1）n+1（1+2+3+…+n）=（-1）n+1•
| n(n+1) |
| 2 |
∴照此规律，第n个等式可为12-22+32-42+…+（-1）n+1n2=（-1）n+1•
| n(n+1) |
| 2 |
点评：本题考查的是归纳推理，要难点在于发现其中的规律，要注意从运算的过程中去寻找，本题属于中档题．
练习册系列答案
相关题目
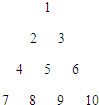把正整数按上小下大、左小右大的原则排成如图三角形数表（每行比上一行多一个数）：设ai，j（i、j∈N*）是位于这个三角形数表中从上往下数第i行、从左往右数第j个数，如a4，2=8，则a51，25为
已知定义在R上的奇函数f（x）满足f（x+1）=f（x），当0＜x＜
时，f（x）=4x，则f（-
）=（ ）
| 1 |
| 2 |
| 5 |
| 4 |
A、-
| ||||
B、-
| ||||
| C、-1 | ||||
D、
|