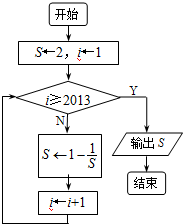
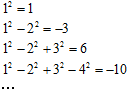题目内容
已知函数f(x)=ex,g(x)=ax2+bx+1(a,b∈R).
(Ⅰ)当a≠0时,若曲线y=f(x)与y=g(x)在x=0出有相同的切线,求b的值;
(Ⅱ)当a=0时,若f(x)≥g(x)对任意的x∈R恒成立,求b的取值范围.
(Ⅰ)当a≠0时,若曲线y=f(x)与y=g(x)在x=0出有相同的切线,求b的值;
(Ⅱ)当a=0时,若f(x)≥g(x)对任意的x∈R恒成立,求b的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(Ⅰ)当a≠0时,求出曲线y=f(x)与y=g(x)在x=0处的切线方程,即可求b的值;
(Ⅱ)当a=0时,φ(x)=f(x)-g(x)=ex-bx-1,所以φ'(x)=ex-b,分类讨论,确定函数的单调性,即可求b的取值范围.
(Ⅱ)当a=0时,φ(x)=f(x)-g(x)=ex-bx-1,所以φ'(x)=ex-b,分类讨论,确定函数的单调性,即可求b的取值范围.
解答:
解:(Ⅰ)因为f'(x)=ex,所以f'(0)=1,又f(0)=1,
得y=f(x)在x=0处的切线方程为y=x+1,…(2分)
又因为g'(x)=2ax+b,所以g'(0)=b,又g(0)=1,
得y=g(x)在x=0处的切线方程为y=bx+1,
因为曲线y=f(x)与y=g(x)在x=0处有相同的切线,所以b=1.…(4分)
(Ⅱ)由a=0,则φ(x)=f(x)-g(x)=ex-bx-1,所以φ'(x)=ex-b,
(i)当b≤0时,φ'(x)>0,函数φ(x)在R上单调递增,
又φ(0)=0,所以当x∈(-∞,0)时,φ(x)<0,与函数f(x)≥g(x)矛盾,…(6分)
(ii)当b>0时,由φ'(x)>0,得x>lnb;由φ'(x)<0,得x<lnb,
所以函数φ(x)在(-∞,lnb)上单调递减,在(lnb,+∞)上单调递增,…(8分)
①当0<b<1时,lnb<0,又φ(0)=0,φ(lnb)<0,与函数f(x)≥g(x)矛盾;
②当b>1时,同理φ(lnb)<0,与函数f(x)≥g(x)矛盾;
③当b=1时,lnb=0,所以函数φ(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,φ(x)≥φ(0)=0,故b=1满足题意.
综上所述,b的取值的范围为{1}.…(12分)
得y=f(x)在x=0处的切线方程为y=x+1,…(2分)
又因为g'(x)=2ax+b,所以g'(0)=b,又g(0)=1,
得y=g(x)在x=0处的切线方程为y=bx+1,
因为曲线y=f(x)与y=g(x)在x=0处有相同的切线,所以b=1.…(4分)
(Ⅱ)由a=0,则φ(x)=f(x)-g(x)=ex-bx-1,所以φ'(x)=ex-b,
(i)当b≤0时,φ'(x)>0,函数φ(x)在R上单调递增,
又φ(0)=0,所以当x∈(-∞,0)时,φ(x)<0,与函数f(x)≥g(x)矛盾,…(6分)
(ii)当b>0时,由φ'(x)>0,得x>lnb;由φ'(x)<0,得x<lnb,
所以函数φ(x)在(-∞,lnb)上单调递减,在(lnb,+∞)上单调递增,…(8分)
①当0<b<1时,lnb<0,又φ(0)=0,φ(lnb)<0,与函数f(x)≥g(x)矛盾;
②当b>1时,同理φ(lnb)<0,与函数f(x)≥g(x)矛盾;
③当b=1时,lnb=0,所以函数φ(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,φ(x)≥φ(0)=0,故b=1满足题意.
综上所述,b的取值的范围为{1}.…(12分)
点评:本题考查利用导数求闭区间上函数的最值,考查利用导数研究曲线上某点切线方程,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目