题目内容
下列结论错误的是( )
| A、a>b,c>d⇒a+c>b+d | ||||
B、当a>b,ab>0时,
| ||||
C、当a,b∈R时,
| ||||
| D、a>b,c>d⇒ac>bd |
考点:不等式的基本性质
专题:不等式的解法及应用
分析:A.a>b,利用基本不等式的性质可得c>d⇒a+c>b+d;
B.a>b,ab>0时,利用基本不等式的性质可得
>
即
<
;
C.当a,b∈R时,利用基本不等式的性质可得
≥ab;
D.例如取a=2,b=1,c=-3,d=-4.
B.a>b,ab>0时,利用基本不等式的性质可得
| a |
| ab |
| b |
| ab |
| 1 |
| a |
| 1 |
| b |
C.当a,b∈R时,利用基本不等式的性质可得
| a2+b2 |
| 2 |
D.例如取a=2,b=1,c=-3,d=-4.
解答:
解:A.a>b,c>d⇒a+c>b+d,正确;
B.a>b,ab>0时,
>
即
<
正确;
C.当a,b∈R时,
≥ab,正确;
D.a>b,c>d⇒ac>bd,不正确,例如取a=2,b=1,c=-3,d=-4.
故选:D.
B.a>b,ab>0时,
| a |
| ab |
| b |
| ab |
| 1 |
| a |
| 1 |
| b |
C.当a,b∈R时,
| a2+b2 |
| 2 |
D.a>b,c>d⇒ac>bd,不正确,例如取a=2,b=1,c=-3,d=-4.
故选:D.
点评:本题考查了不等式的基本性质,属于基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
已知f(x)=sinx+cosx,则在[0,2π)内f(x)的单调递减区间为( )
A、[0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
已知函数y=x+2,则y′=( )
| A、x | B、x+2 | C、1 | D、2 |
若函数设f(x)=
为偶函数,则a=( )
| x2+1 |
| (3x+2)(x-a) |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
设一次函数y=kix+bi的图象为li(i=1,2,3,4),如图所示,则有( )
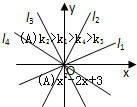

| A、k2>k1>k4>k3 |
| B、k2>k1>k3>k4 |
| C、k1>k2>k3>k4 |
| D、k1>k2>k4>k3 |
