题目内容
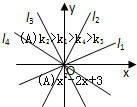
设一次函数y=kix+bi的图象为li（i=1，2，3，4），如图所示，则有（ ）
| A、k2＞k1＞k4＞k3 |
| B、k2＞k1＞k3＞k4 |
| C、k1＞k2＞k3＞k4 |
| D、k1＞k2＞k4＞k3 |
考点：一次函数的性质与图象
专题：函数的性质及应用
分析：根据一次函数图象和性质，当函数为增函数时斜率k＞0，当函数为减函数时斜率k＜0，图象与y轴夹角越小，|k|越大，可得答案．
解答：
解：由已知中一次函数y=kix+bi的图象为li（i=1，2，3，4），
可得：k2＞k1＞0＞k4＞k3，
故选：A
可得：k2＞k1＞0＞k4＞k3，
故选：A
点评：本题考查的知识点是一次函数的图象和性质，熟练掌握一次函数图象与性质的关系是解答的关键．
练习册系列答案
相关题目
下列结论错误的是（ ）
| A、a＞b，c＞d⇒a+c＞b+d | ||||
B、当a＞b，ab＞0时，
| ||||
C、当a，b∈R时，
| ||||
| D、a＞b，c＞d⇒ac＞bd |
定义在R上的奇函数f（x）在[0+∞）上是增函数，又f（x）+f（1-2x）＞0，则x的取值范围是（ ）
A、（-∞，
| ||
B、（
| ||
| C、（-∞，1） | ||
| D、（1，+∞） |
M={x||x|≤2}，N={x|a-1≤x≤a+1}，若N是M的真子集，则a的取值范围是（ ）
| A、（-1，1） |
| B、[-1，1] |
| C、（-1，1] |
| D、[-1，1） |
已知全集I={1，2，3，4，5，6}，集合A={2，3，5，6}，B={1，3}，则（∁IA）∪B为（ ）
| A、{3} |
| B、{1，3} |
| C、{3，4} |
| D、{1，3，4} |
函数f（x）=
+lg（x-1）的定义域是（ ）
| 1 | ||
|
| A、（1，+∞） |
| B、（3，+∞） |
| C、（1，3） |
| D、[3，+∞） |