题目内容

已知复数z=a+bi（a，b∈R），且a2-（i-1）a+3b+2i=0
（1）求复数z；
（2）若z+
m
z
为实数，求实数m的值．
考点：复数代数形式的混合运算
专题：数系的扩充和复数
分析：（1）由a2-（i-1）a+3b+2i=0求得a，b的值，则复数z可求；
（2）把z代入z+
m
z
，由z+
m
z
为实数列式求得实数m的值．
解答： 解：（1）由a2-（i-1）a+3b+2i=0，
得a2+a+3b+（2-a）i=0．
∴
a2+a+3b=0
2-a=0
．
解得：
a=2
b=-2
．
∴z=2-2i
（2）∵z+
m
z
=2-2i+
m
2-2i

=2-2i+
m(2+2i)
(2-2i)(2+2i)
=2-2i+
m+mi
4

=
8+m
4
+
m-8
4
i．
∵z+
m
z
为实数
∴
m-8
4
=0．
解得：m=8．
点评：本题考查了复数代数形式的混合运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
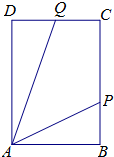如图，ABCD是长方形海域，其中AB=10海里，AD=10
2
海里．现有一架飞机在该海域失事，两艘海事搜救船在A处同时出发，沿直线AP、AQ向前联合搜索，且∠PAQ=
π
4
（其中P、Q分别在边BC、CD上），搜索区域为平面四边形APCQ围成的海平面．设∠PAB=θ，搜索区域的面积为S． 
（1）试建立S与tanθ的关系式，并指出tanθ的取值范围；
（2）求S的最大值，并指出此时θ的值．
已知函数f（x）=
(x-2m)2
lnx
（其中m为常数）．
（Ⅰ）当m=0时，求函数f（x）的单调区间；
（Ⅱ）当0＜m＜
1
2
时，设函数f（x）的3个极值点为a，b，c，且a＜b＜c．证明：a+c＞
2
e
．
如图，在五棱锥S-ABCDE中，SA⊥底面ABCDES，SA=AB=AE=2，BC=DE=
3
，SC=
11
，∠BAE=∠BCD=∠CDE=120° 
（Ⅰ））证明BC⊥平面SAB；
（Ⅱ）求SC与面ABCDE所成的角的正弦值．
已知曲线C1的极坐标方程为ρcos（θ-
π
3
）=-1，曲线C2的极坐标方程为ρ=2
2
cos（θ-
π
4
）．以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系．
（1）求曲线C2的直角坐标方程；
（2）求曲线C2上的动点M到曲线C1的距离的最大值．
某中学一名数学老师对全班50名学生某次考试成绩分男女生进行了统计，其中120分（含120分）以上为优秀，绘制了如下的两个频率分布直方图：

（1）根据以上两个直方图完成下面的2×2列联表：
成绩性别优秀不优秀总计
男生
女生
总计
（2）根据（1）中表格的数据计算，你有多大把握认为学生的数学成绩与性别之间有关系？
（注：
k02.0722.7063.8415.0246.6357.87910.828
P（K2≥k0）0.150.100.050.0250.0100.0050.001
K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)
，其中n=a+b+c+d）
（3）若从成绩在[130，140]的学生中任取2人，求取到的2人中至少有1名女生的概率．
已知（x
x
+
1
3x
）n的展开式中，前三项的二项式系数之和为37．
（Ⅰ）求n的值；    
（Ⅱ）求x的整数次幂的项．
已知函数f(x)=
ax
x2+b
在x=-1处取得极值-2．
（Ⅰ）求函数f（x）的表达式；
（Ⅱ）求函数f（x）单调区间．
我国政府对PM2.5采用如下标准：
PM2.5日均值m（微克/立方米）空气质量等级
m＜35一级
35≤m≤75二级
m＞75超标
某市环保局从180天的市区PM2.5监测数据中，随机抽取l0天的数据作为样本，监测值如茎叶图所示（十位为茎，个位为叶）．
（Ⅰ）求这10天数据的中位数．
（Ⅱ）从这l0天的数据中任取3天的数据，记ξ表示空气质量达到一级的天数，求ξ的分布列；
（Ⅲ）以这10天的PM2.5日均值来估计这180天的空气质量情况，记η为这180天空气质量达到一级的天数，求η的均值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网