题目内容
6.正整数列{an},{bn}满足:a1≥b1,且对一切k≥2,k∈N*,ak是ak-1与bk-1的等差中项,bk是ak-1与bk-1的等比中项.(1)若a2=2,b2=1,求a1,b1的值;
(2)求证:{an}是等差数列的充要条件是{an}为常数数列;
(3)记cn=|an-bn|,当n≥2(n∈N*)时,指出c2+…+cn与c1的大小关系并说明理由.
分析 (1)正整数列{an},{bn}满足:a1≥b1,且对一切k≥2,k∈N*,ak是ak-1与bk-1的等差中项,bk是ak-1与bk-1的等比中项.可得2ak=ak-1+bk-1,bk2=ak-1bk-1,对k取值即可得出.
(2){an}是等差数列,2ak=ak-1+bk-1,2ak=ak-1+ak+1,可得bk-1=ak+1,bk=ak+2,bk2=ak-1bk-1,ak+22=ak-1ak+1,k=2时,a42=a1a3,(a1+3d)2=a1(a1+2d),可得d=0.即可证明.
(3)对一切k≥2,k∈N*,ak是ak-1与bk-1的等差中项,bk是ak-1与bk-1的等比中项.2an=an-1+bn-1,bn2=an-1bn-1,利用基本不等式的性质可得an=$\frac{{a}_{n-1}+{b}_{n-1}}{2}$$≥\sqrt{{a}_{n-1}{b}_{n-1}}$=$\sqrt{{b}_{n}^{2}}$=bn,cn=|an-bn|=an-bn.可得an+1-bn+1=$\frac{{a}_{n}+{b}_{n}}{2}$-$\sqrt{{a}_{n}{b}_{n}}$=$\frac{1}{2}({a}_{n}+{b}_{n}-2\sqrt{{a}_{n}{b}_{n}})$≤$\frac{1}{2}$(an+bn-2bn)=$\frac{1}{2}({a}_{n}-{b}_{n})$,即${c}_{n+1}≤\frac{1}{2}{c}_{n}$.利用等比数列的求和公式即可得出.
解答 解:(1)正整数列{an},{bn}满足:a1≥b1,且对一切k≥2,k∈N*,
ak是ak-1与bk-1的等差中项,bk是ak-1与bk-1的等比中项.
∴2ak=ak-1+bk-1,bk2=ak-1bk-1,
a2=2,b2=1,可得4=a1+b1,1=a1b1,
解得a1=2+$\sqrt{3}$,b1=2-$\sqrt{3}$.
(2)证明:{an}是等差数列,2ak=ak-1+bk-1,2ak=ak-1+ak+1,可得bk-1=ak+1,
则bk=ak+2,∵bk2=ak-1bk-1,
∴ak+22=ak-1ak+1,k=2时,a42=a1a3,(a1+3d)2=a1(a1+2d),
6a1d+9d2=2a1d,即d(4a1+9d)=0,正整数列{an},可知d≥0,4a1+9d>0,∴d=0.
∴数列{an}为常数数列.
{an}是等差数列的充要条件是{an}为常数数列.
(3)对一切k≥2,k∈N*,ak是ak-1与bk-1的等差中项,bk是ak-1与bk-1的等比中项.
2an=an-1+bn-1,bn2=an-1bn-1,
∴an=$\frac{{a}_{n-1}+{b}_{n-1}}{2}$$≥\sqrt{{a}_{n-1}{b}_{n-1}}$=$\sqrt{{b}_{n}^{2}}$=bn,
又已知a1≥b1,
∴cn=|an-bn|=an-bn.
∴an+1-bn+1=$\frac{{a}_{n}+{b}_{n}}{2}$-$\sqrt{{a}_{n}{b}_{n}}$=$\frac{1}{2}({a}_{n}+{b}_{n}-2\sqrt{{a}_{n}{b}_{n}})$≤$\frac{1}{2}$(an+bn-2bn)=$\frac{1}{2}({a}_{n}-{b}_{n})$,
即${c}_{n+1}≤\frac{1}{2}{c}_{n}$.
∴${c}_{n}≤\frac{1}{2}{c}_{n-1}$$≤\frac{1}{{2}^{2}}{c}_{n-2}$≤…≤$\frac{1}{{2}^{n-1}}{c}_{1}$,
∴c2+…+cn≤$\frac{1}{2}{c}_{1}+\frac{1}{{2}^{2}}{c}_{1}$+…+$\frac{1}{{2}^{n-1}}{c}_{1}$=$(1-\frac{1}{{2}^{n-1}}){c}_{1}$≤c1.
∴当n≥2(n∈N*)时,c2+…+cn≤c1.
点评 本题考查了等差数列与等比数列的通项公式、基本不等式的性质、数列的单调性,考查了推理能力与计算能力,属于难题.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | -6 | B. | 6 | C. | 7 | D. | 8 |
| A. | (-2,0) | B. | (0,-2) | C. | (2,0) | D. | (0,2) |
| A. | $(-∞,\frac{{\sqrt{e}}}{e}-8]$ | B. | $[\frac{{\sqrt{e}}}{e}-8,+∞)$ | C. | $[\sqrt{2},e)$ | D. | $(-\frac{{\sqrt{3}}}{3},\frac{e}{2}]$ |
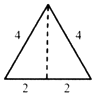
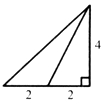
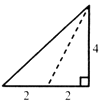
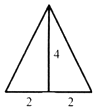
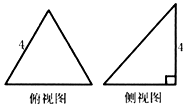 已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )
已知三棱锥的俯视图与侧视图如图所示,俯视图是边长为4的正三角形,侧视图是有一直角边长为4的直角三角形,则该三棱锥的正视图可能是( )