题目内容
16.已知O是坐标原点,点A(-1,0),若M(x,y)为平面区域$\left\{\begin{array}{l}{x+y≥2}\\{x≤1y≤2}\\{\;}\end{array}\right.$上的一个动点,则|$\overrightarrow{OA}+\overrightarrow{OM}$|的取值范围是[1,$\sqrt{5}$].分析 由题意作出可行域,由向量的坐标加法运算求得+的坐标,把||转化为可行域内的点M(x,y)到定点N(1,0)的距离,数形结合可得答案.
解答 解:$\overrightarrow{OA}+\overrightarrow{OM}$=(-1,0)+(x,y)=(x-1,y),
则|$\overrightarrow{OA}+\overrightarrow{OM}$|=$\sqrt{(x-1)^{2}+{y}^{2}}$,
设z=|$\overrightarrow{OA}+\overrightarrow{OM}$|=$\sqrt{(x-1)^{2}+{y}^{2}}$,
则z的几何意义为M到定点D(1,0)的距离,
由约束条件作平面区域如图,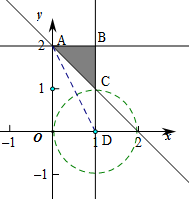
由图象可知当M位于A(0,2)时,z取得最大值z=$\sqrt{1+4}$=$\sqrt{5}$,
当M位于C(1,1)时,z取得最小值z=1,
1≤z≤$\sqrt{5}$,
即$\sqrt{(x-1)^{2}+{y}^{2}}$的取值范围是[1,$\sqrt{5}$],
故答案为:[1,$\sqrt{5}$].
点评 本题考查了简单的线性规划,考查了数形结合、转化与化归等解题思想方法,考查了向量模的求法,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.双曲线 $\frac{x^2}{4}-\frac{y^2}{16}=1$的一条渐近线方程为( )
| A. | y=2x | B. | $y=\frac{1}{2}x$ | C. | y=4x | D. | $y=\frac{1}{4}x$ |
8.若实数x,y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$,则目标函数z=2x+y的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |