题目内容

17．“sinα=cosα”是“$α=\frac{π}{4}+2kπ，（k∈Z）$”的（　　）
A．充分不必要条件B．必要不充分条件
C．充分必要条件D．既不充分也不必要条件

分析 根据充分必要条件的定义结合集合的包含关系判断即可．

解答 解：由“sinα=cosα”得：α=kπ+$\frac{π}{4}$，k∈Z，
故sinα=cosα是“$α=\frac{π}{4}+2kπ，（k∈Z）$”的必要不充分条件，
故选：B．

点评 本题考查了充分必要条件，考查三角函数以及集合的包含关系，是一道基础题．

练习册系列答案
相关题目
7．已知函数f（x）=$\frac{sin2x（sinx+cosx）}{cosx}$=$\sqrt{2}$sin（2x-$\frac{π}{4}$）+1．
（1）求函数f（x）的单调递减区间；
（2）求f（x）在区间[-$\frac{π}{6}$，$\frac{π}{4}$]上的最大值和最小值．
8．若实数x，y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$，则目标函数z=2x+y的最小值为（　　）
A．$\frac{1}{3}$B．$\frac{1}{2}$C．1D．2
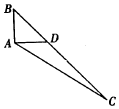5．设数列{an}为等差数列，且a11=$\frac{π}{2}$，若f（x）=sin2x+2cos2$\frac{x}{2}$，记bn=f（an），则数列{bn}的前21项和为21．
12．如图，在△ABC中，AD⊥AB，$\overrightarrow{BC}$=3$\overrightarrow{BD}$，|$\overrightarrow{AD}$|=1，则$\overrightarrow{AC}$•$\overrightarrow{AD}$的值为（　　）
A．1B．2C．3D．4
2．某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，可见部分如下，据此解答下列问题：

（Ⅰ）求全班人数及分数在[80，90）之间的频数；
（Ⅱ）若要从分数在[90，100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份在[90，100]之间的概率．
9．已知函数f（x）=ax3+x，g（x）=x2+px+q．
（Ⅰ）若函数f（x）在x=1处取得极值，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，函数F（x）=f'（x）g（x）（其中f'（x）为函数f（x）的导数）的图象关于直线x=-1对称，求函数F（x）单调区间；
（Ⅲ）在（Ⅱ）的条件下，若对任意的x≥1，都有g（x）≥（6+λ）x-λlnx+3恒成立，求实数λ的取值范围．
6．正整数列{an}，{bn}满足：a1≥b1，且对一切k≥2，k∈N*，ak是ak-1与bk-1的等差中项，bk是ak-1与bk-1的等比中项．
（1）若a2=2，b2=1，求a1，b1的值；
（2）求证：{an}是等差数列的充要条件是{an}为常数数列；
（3）记cn=|an-bn|，当n≥2（n∈N*）时，指出c2+…+cn与c1的大小关系并说明理由．
16．设a，b∈R，c∈[0，2π），若对任意实数x都有2sin（3x-$\frac{π}{3}$）=asin（bx+c），定义在区间[0，3π]上的函数y=sin2x的图象与y=cosx的图象的交点横坐标为d，则满足条件的有序实数组（a，b，c，d）的组数为28．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网