设变量x.y满足约束条件$\left\{\begin{array}{l}3x+y-6≥0\\ x-y-2≤0\\ y-3≤0\end{array}\right.$.则目标函数z=4x+y的最小值为( )A．-6B．6C．7D．8 题目和参考答案——青夏教育精英家教网——

题目内容

14．设变量x、y满足约束条件$\left\{\begin{array}{l}3x+y-6≥0\\ x-y-2≤0\\ y-3≤0\end{array}\right.$，则目标函数z=4x+y的最小值为（　　）

A．

-6

B．

6

C．

7

D．

8

分析画出约束条件的可行域，利用目标函数的几何意义求解即可．

解答解：由x，y满足的约束条件$\left\{\begin{array}{l}3x+y-6≥0\\ x-y-2≤0\\ y-3≤0\end{array}\right.$，画出可行域如图所示，
当直线z=4x+y过点C（1，3）时，z取得最小值且最小值为4+3=7．

故选：C．

点评本题考查线性规划的简单应用，考查数形结合思想以及转化思想的应用，考查计算能力．

练习册系列答案

名校有约小学毕业升学总复习系列答案

初中毕业升学考试指南系列答案

组合阅读训练系列答案

名校名师测试卷系列答案

期末复习第1卷系列答案

初中毕业生升学考试复习用书系列答案

阶段性同步复习与测试系列答案

创新学案课时作业测试卷系列答案

学与练阅读与写作系列答案

巧学蛙课堂全解系列答案

相关题目

4．给出下列四个命题：
①函数y=$\frac{1}{x}$的单调减区间是（-∞，0）∪（0，+∞）；
②函数y=2x（x∈N）的图象是一直线；
③函数y=3（x-1）²的图象可由y=3x²的图象向右平移1个单位得到；
④若函数f（x）的定义域为[0，2]，则函数f（2x）的定义域为[0，1]；
其中正确命题的序号是③④．（填上所有正确命题的序号）

5．设数列{a_n}为等差数列，且a₁₁=$\frac{π}{2}$，若f（x）=sin2x+2cos²$\frac{x}{2}$，记b_n=f（a_n），则数列{b_n}的前21项和为21．

2．某校高三（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏，可见部分如下，据此解答下列问题：

（Ⅰ）求全班人数及分数在[80，90）之间的频数；
（Ⅱ）若要从分数在[90，100]之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份在[90，100]之间的概率．

9．已知函数f（x）=ax³+x，g（x）=x²+px+q．
（Ⅰ）若函数f（x）在x=1处取得极值，求实数a的值；
（Ⅱ）在（Ⅰ）的条件下，函数F（x）=f'（x）g（x）（其中f'（x）为函数f（x）的导数）的图象关于直线x=-1对称，求函数F（x）单调区间；
（Ⅲ）在（Ⅱ）的条件下，若对任意的x≥1，都有g（x）≥（6+λ）x-λlnx+3恒成立，求实数λ的取值范围．

19．“$\frac{1}{x}＞1$”是“e^x-1＜1”的（　　）

	A．	充分且不必要条件		B．	必要且不充分条件
	C．	充要条件		D．	既非充分也非必要条件

6．正整数列{a_n}，{b_n}满足：a₁≥b₁，且对一切k≥2，k∈N^*，a_k是a_k-1与b_k-1的等差中项，b_k是a_k-1与b_k-1的等比中项．
（1）若a₂=2，b₂=1，求a₁，b₁的值；
（2）求证：{a_n}是等差数列的充要条件是{a_n}为常数数列；
（3）记c_n=|a_n-b_n|，当n≥2（n∈N^*）时，指出c₂+…+c_n与c₁的大小关系并说明理由．

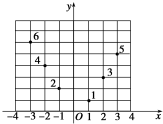如图所示，坐标纸上的每个单元格的边长为1，由下往上的六个点：1，2，3，4，5，6的横、纵坐标分别对应数列{a_n}（n∈N^*）的前12项，如表所示．

a₁	a₂	a₃	a₄	a₅	a₆	a₇	a₈	a₉	a₁₀	a₁₁	a₁₂
x₁	y₁	x₂	y₂	x₃	y₃	x₄	y₄	x₅	y₅	x₆	y₆

按如此规律下去，则a₂₀₀₉+a₂₀₁₀+a₂₀₁₁等于（　　）

13．（1）用辗转相除法求840与1 764 的最大公约数；
（2）把666_（7）化为十进制，把342_（10）化为八进制．