题目内容
(理科)甲、乙两人进行投篮训练,甲投进的概率为
,乙投进的概率为
,两人投进与否要睛互没有影响.
(Ⅰ)两人各投1次,求恰有1人投进的概率;
(Ⅱ)若随机变量ξ表示乙投篮3次后投进的总次数,求ξ的分布列及数学期望Eξ.
| 2 |
| 5 |
| 3 |
| 4 |
(Ⅰ)两人各投1次,求恰有1人投进的概率;
(Ⅱ)若随机变量ξ表示乙投篮3次后投进的总次数,求ξ的分布列及数学期望Eξ.
考点:离散型随机变量的期望与方差,互斥事件与对立事件,相互独立事件的概率乘法公式,离散型随机变量及其分布列
专题:计算题
分析:(I)记“甲投篮1次投进”为事件A,“乙投篮1次投进”为事件B,“两人各投1次,恰有1人投进”为事件C,则事件C包括甲中已不中,甲不中乙中.由题意可得事件A,B是相互独立事件,进而根据相互独立事件的概率乘法公式求出答案.
(Ⅱ)随机变量ξ表示乙投篮3次后投进的总次数,可能取值为0,1,2,3,则ξ~B(3,
),根据二项分别的概率和期望公式可得到答案.
(Ⅱ)随机变量ξ表示乙投篮3次后投进的总次数,可能取值为0,1,2,3,则ξ~B(3,
| 3 |
| 4 |
解答:
解:(I)记“甲投篮1次投进”为事件A,“乙投篮1次投进”为事件B,“两人各投1次,恰有1人投进”为事件C,
所以P(A)=
,P(B)=
,
根据相互独立事件的概率乘法公式可得:P(C)=P(A•
)+P(
• B)=
×(1-
)+(1-
)×
=
,
所以甲投进而乙未投进的概率为
.
(Ⅱ)随机变量ξ表示乙投篮3次后投进的总次数,可能取值为0,1,2,3,则ξ~B(3,
)
∴P(ξ=k)=
(
)k(
) 3-k(k=0,1,2,3)
数学期望Eξ=nP(B)=3×
=
所以P(A)=
| 2 |
| 5 |
| 3 |
| 4 |
根据相互独立事件的概率乘法公式可得:P(C)=P(A•
. |
| B |
. |
| A |
| 2 |
| 5 |
| 3 |
| 4 |
| 2 |
| 5 |
| 3 |
| 4 |
| 11 |
| 20 |
所以甲投进而乙未投进的概率为
| 11 |
| 20 |
(Ⅱ)随机变量ξ表示乙投篮3次后投进的总次数,可能取值为0,1,2,3,则ξ~B(3,
| 3 |
| 4 |
∴P(ξ=k)=
| C | k 3 |
| 3 |
| 4 |
| 1 |
| 4 |
数学期望Eξ=nP(B)=3×
| 3 |
| 4 |
| 9 |
| 4 |
点评:本题以投篮为素材,考查相互独立事件的定义与计算公式,考查二项分布.解决此题的关键是首先明确事件之间的关系,即是独立关系还是相互独立关系,进而选择正确的公式进行解题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
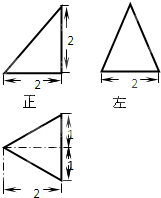
已知某个几何体的三视图如右,那么可得这个几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
已知实数k满足
>1.则方程x2-kx+1=0的两个根可分别作为( )
| 1 |
| k-2 |
| A、一椭圆和一双曲线的离心率 |
| B、两抛物线的离心率 |
| C、一椭圆和一抛物线的离心率 |
| D、两椭圆的离心率 |
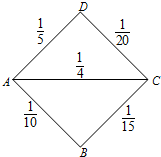 某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位C处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如下图(例如,路段AB发生堵车事件的概率为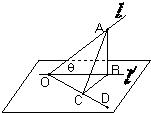 如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.
如图,l是平面α的斜线,斜足是O,A是l上任意一点,AB是平面α的垂线,B是垂足,设OD是平面α内与OB不同的一条直线,AC垂直于OD于C,若直线l与平面α所成的角θ=45°,∠BOC=45°,求∠AOC的大小.