题目内容
f(x)=
,
(1)试根据c不同取值,讨论f2(x)+f(x)+c=0的实数解的个数;
(2)试根据b不同取值,讨论f2(x)+bf(x)+1=0的实数解的个数.
|
(1)试根据c不同取值,讨论f2(x)+f(x)+c=0的实数解的个数;
(2)试根据b不同取值,讨论f2(x)+bf(x)+1=0的实数解的个数.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:(1)(2)通过f(x)的解的个数,判别式△判断方程的解的情况.
解答:
解:(1)先根据题意作出f(x)的简图:
∴f(x)=0有3个解,x=0,x=1,x=2,
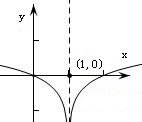 由题意,对于f2(x)+f(x)+c=0来说,
由题意,对于f2(x)+f(x)+c=0来说,
△=1-4c>0,即c<
时,有5个解,
△=1-4c=0,即c=
时,有3个解,
△=1-4c<0,即c>
时,无解;
(2)由(1)得:f(x)=0有3个解,x=0,x=1,x=2,
由题意,对于f2(x)+bf(x)+1=0来说,
△=b2-4>0,即b>2或b<-2时,有5个解,
△=b2-4=0,即b=2或b=-2时,有3个解,
△=b2-4<0,即-2b<2时,无解,
∴f(x)=0有3个解,x=0,x=1,x=2,
 由题意,对于f2(x)+f(x)+c=0来说,
由题意,对于f2(x)+f(x)+c=0来说,△=1-4c>0,即c<
| 1 |
| 4 |
△=1-4c=0,即c=
| 1 |
| 4 |
△=1-4c<0,即c>
| 1 |
| 4 |
(2)由(1)得:f(x)=0有3个解,x=0,x=1,x=2,
由题意,对于f2(x)+bf(x)+1=0来说,
△=b2-4>0,即b>2或b<-2时,有5个解,
△=b2-4=0,即b=2或b=-2时,有3个解,
△=b2-4<0,即-2b<2时,无解,
点评:数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
函数f(x)是定义在R上的偶函数,且满足f(x+2)=f(x),当x∈[0,1]时,f(x)=2x.若在区间[-2,2]上方程ax+a-f(x)=0恰有三个不相等的实数根,则实数a的取值范围是( )
| A、[0,1) |
| B、[0,2] |
| C、[1,+∞) |
| D、[2,+∞) |
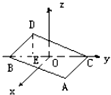 如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(
如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(