题目内容
已知函数f（x）=2sin2（x+
）-
cos2x，x∈[
，
]．设x=α时f（x）取到最大值．
（1）求f（x）的最大值及α的值；
（2）在△ABC中，角A，B，C所对的边分别为a，b，c，A=α-
，且sinBsinC=sin2A，试判断三角形的形状．
| π |
| 4 |
| 3 |
| π |
| 4 |
| π |
| 2 |
（1）求f（x）的最大值及α的值；
（2）在△ABC中，角A，B，C所对的边分别为a，b，c，A=α-
| π |
| 12 |
考点：三角函数中的恒等变换应用,余弦定理
专题：三角函数的求值
分析：（1）化简函数的解析式为f（x）=1+2sin（2x-
），根据x∈[
，
]，利用正弦函数的定义域和值域求得f（x）的最大值以及此时a的值．
（2）由（1）知A=α-
=
，由sinBsinC=sin2A，可得bc=a2．又由余弦定理可得 （b-c）2=0，故有 b=c，三角形为等边三角形．
| π |
| 3 |
| π |
| 4 |
| π |
| 2 |
（2）由（1）知A=α-
| π |
| 12 |
| π |
| 3 |
解答：
解：（1）依题函数f（x）=2sin2（x+
）-
cos2x=[1-cos（2x+
]-
cos2x=1+sin2x-
cos2x=1+2sin（2x-
），
∵x∈[
，
]，则
≤2x-
≤
，故当 2x-
=
，即x=α=
时，f（x）取得最大值为3．
（2）由（1）知A=α-
=
，由sinBsinC=sin2A，可得bc=a2，
又由余弦定理可得a2=b2+c2-2bc•cosA=b2+c2-bc，∴（b-c）2=0，∴b=c，
又 A=α-
=
，所以三角形为等边三角形．
| π |
| 4 |
| 3 |
| π |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
∵x∈[
| π |
| 4 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
（2）由（1）知A=α-
| π |
| 12 |
| π |
| 3 |
又由余弦定理可得a2=b2+c2-2bc•cosA=b2+c2-bc，∴（b-c）2=0，∴b=c，
又 A=α-
| π |
| 12 |
| π |
| 3 |
点评：本题主要考查三角函数的恒等变换及化简求值，正弦函数的定义域和值域，余项定理的应用，属于基础题．
练习册系列答案
相关题目
函数f（x）是定义在R上的偶函数，且满足f（x+2）=f（x），当x∈[0，1]时，f（x）=2x．若在区间[-2，2]上方程ax+a-f（x）=0恰有三个不相等的实数根，则实数a的取值范围是（ ）
| A、[0，1） |
| B、[0，2] |
| C、[1，+∞） |
| D、[2，+∞） |
定义在R上的偶函数f（x）满足：对任意的x1，x2∈（-∞，0]（x1≠x2），有（x1-x2）•（f（x1）-f（x2））＞0，则当n∈N*时，有（ ）
| A、f（-n）＜f（n-1）＜f（n+1） |
| B、f（n-1）＜f（-n）＜f（n+1） |
| C、f（n+1）＜f（n-1）＜f（-n） |
| D、f（n+1）＜f（-n）＜f（n-1） |
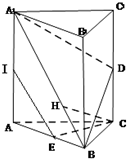如图，在三棱柱ABC-A1B1C1中，△ABC是边长为2的等边三角形，AA1⊥平面ABC，D，E，I分别是CC1，AB，AA1的中点．
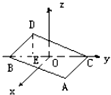如图，在空间直角坐标系中，BC=2，原点O是BC的中点，点A的坐标是（