题目内容
设a∈R,函数f(x)=lnx-ax.
(1)若a=3,求曲线y=f(x)在P(1,-3)处的切线方程;
(2)若f(x)有零点,求实数a的取值范围;
(3)若f(x)有两个相异零点x1,x2,求证:x1•x2>e2.
(1)若a=3,求曲线y=f(x)在P(1,-3)处的切线方程;
(2)若f(x)有零点,求实数a的取值范围;
(3)若f(x)有两个相异零点x1,x2,求证:x1•x2>e2.
考点:利用导数研究曲线上某点切线方程,函数零点的判定定理
专题:计算题,证明题,导数的综合应用
分析:(1)求出当a=3 时的导数,再求切线的斜率,由点斜式方程,即可得到切线方程;
(2)对a讨论,分a=0,a<0,a>0,可通过解方程和零点存在定理以及应用导数求极值,令极大值不小于0,即可得到;
(3)原不等式x1x2>e2?lnx1+lnx2>2?a(x1+x2)>2?
>
?ln
>
,
令
=t,则t>1,于是ln
>
?lnt>
.设函数g(t)=lnt-
(t>1).求出导数,判断单调性,由单调性即可得证.
(2)对a讨论,分a=0,a<0,a>0,可通过解方程和零点存在定理以及应用导数求极值,令极大值不小于0,即可得到;
(3)原不等式x1x2>e2?lnx1+lnx2>2?a(x1+x2)>2?
| lnx1-lnx2 |
| x1-x2 |
| 2 |
| x1+x2 |
| x1 |
| x2 |
| 2(x1-x2) |
| x1+x2 |
令
| x1 |
| x2 |
| x1 |
| x2 |
| 2(x1-x2) |
| x1+x2 |
| 2(t-1) |
| t+1 |
| 2(t-1) |
| t+1 |
解答:
解:在区间(0,+∞)上,f′(x)=
-a=
.
(1)当a=3 时,f'(x)=
-3.
曲线y=f(x)在P(1,-3)处的切线斜率为1-3=-2,
则切线方程为y-(-3)=-2(x-1),即2x+y+1=0;
(2)①若a=0,f(x)=lnx有唯一零点x=1.
②若a<0,则f′(x)>0,f(x)是区间(0,+∞)上的增函数,
∵f(1)=-a>0,f(ea)=a-aea=a(1-ea)<0,
∴f(1)•f(ea)<0,函数f(x)在区间(0,+∞)有唯一零点.
③若a>0,令f′(x)=0得:x=
.
在区间(0,
)上,f′(x)>0,函数f(x)是增函数;
在区间(
,+∞)上,f′(x)<0,函数f(x)是减函数;
故在区间(0,+∞)上,f(x)的极大值为f(
)=ln
-1=-lna-1.
由f(
)≥0 即-lna-1≥0,解得:a≤
.
故所求实数a的取值范围是(-∞,
].
(3)证明:设x1>x2>0,∵f(x1)=f(x2)=0∴lnx1-ax1=0,lnx2-ax2=0,
∴lnx1+lnx2=a(x1+x2),lnx1-lnx2=a(x1-x2),
原不等式x1x2>e2?lnx1+lnx2>2?a(x1+x2)>2,
?
>
?ln
>
,
令
=t,则t>1,于是ln
>
?lnt>
.
设函数g(t)=lnt-
(t>1).
求导得:g′(t)=
-
=
>0,
故函数g(t)是(1,+∞)上的增函数,
∴g(t)>g(1)=0,即不等式lnt>
(t>1)成立,
故所证不等式x1•x2>e2成立.
| 1 |
| x |
| 1-ax |
| x |
(1)当a=3 时,f'(x)=
| 1 |
| x |
曲线y=f(x)在P(1,-3)处的切线斜率为1-3=-2,
则切线方程为y-(-3)=-2(x-1),即2x+y+1=0;
(2)①若a=0,f(x)=lnx有唯一零点x=1.
②若a<0,则f′(x)>0,f(x)是区间(0,+∞)上的增函数,
∵f(1)=-a>0,f(ea)=a-aea=a(1-ea)<0,
∴f(1)•f(ea)<0,函数f(x)在区间(0,+∞)有唯一零点.
③若a>0,令f′(x)=0得:x=
| 1 |
| a |
在区间(0,
| 1 |
| a |
在区间(
| 1 |
| a |
故在区间(0,+∞)上,f(x)的极大值为f(
| 1 |
| a |
| 1 |
| a |
由f(
| 1 |
| a |
| 1 |
| e |
故所求实数a的取值范围是(-∞,
| 1 |
| e |
(3)证明:设x1>x2>0,∵f(x1)=f(x2)=0∴lnx1-ax1=0,lnx2-ax2=0,
∴lnx1+lnx2=a(x1+x2),lnx1-lnx2=a(x1-x2),
原不等式x1x2>e2?lnx1+lnx2>2?a(x1+x2)>2,
?
| lnx1-lnx2 |
| x1-x2 |
| 2 |
| x1+x2 |
| x1 |
| x2 |
| 2(x1-x2) |
| x1+x2 |
令
| x1 |
| x2 |
| x1 |
| x2 |
| 2(x1-x2) |
| x1+x2 |
| 2(t-1) |
| t+1 |
设函数g(t)=lnt-
| 2(t-1) |
| t+1 |
求导得:g′(t)=
| 1 |
| t |
| 4 |
| (t+1)2 |
| (t-1)2 |
| t(t+1)2 |
故函数g(t)是(1,+∞)上的增函数,
∴g(t)>g(1)=0,即不等式lnt>
| 2(t-1) |
| t+1 |
故所证不等式x1•x2>e2成立.
点评:本题考查导数的运用:求切线方程和求单调区间和极值,考查函数的零点问题,注意运用零点存在定理,考查不等式的证明,注意构造函数应用导数判断单调性加以证明,属于中档题.

练习册系列答案
相关题目
定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x1-x2)•(f(x1)-f(x2))>0,则当n∈N*时,有( )
| A、f(-n)<f(n-1)<f(n+1) |
| B、f(n-1)<f(-n)<f(n+1) |
| C、f(n+1)<f(n-1)<f(-n) |
| D、f(n+1)<f(-n)<f(n-1) |
设函数f(x)=log3
-a在(1,2)内有零点,则实数a的取值范围是( )
| x+2 |
| x |
| A、(0,log32) |
| B、(log32,1) |
| C、(-1,-log32) |
| D、(1,log34) |
设m∈R,则“m<0”是“m<1”的( )
| A、充分必要条件 |
| B、必要而不充分条件 |
| C、充分而不必要条件 |
| D、既不充分也不必要条件 |
对于集合A={2,4,6},若a∈A,则6-a∈A,那么a的值是( )
| A、2 | B、4 | C、6 | D、2或4 |
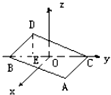 如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(
如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标是(