题目内容
已知f(x)=
,x≥0,若f1(x)=f(x),fn+1(x)=f(fn(x)),n∈N+,则f2014(x)的表达式为 .
| x |
| 1+x |
考点:归纳推理,函数解析式的求解及常用方法
专题:简易逻辑
分析:由题意,可先求出f1(x),f2(x),f3(x)…,归纳出fn(x)的表达式,即可得出f2014(x)的表达式
解答:
解:由题意f1(x)=f(x)=
.
f2(x)=f(f1(x))=
=
.
f3(x)=f(f2(x))=
=
.
…
fn(x)=f(fn-1(x))=…=
故f2014(x)=
故答案为:
| x |
| 1+x |
f2(x)=f(f1(x))=
| ||
1+
|
| x |
| 1+2x |
f3(x)=f(f2(x))=
| ||
1+
|
| x |
| 1+3x |
…
fn(x)=f(fn-1(x))=…=
| x |
| 1+nx |
故f2014(x)=
| x |
| 1+2014x |
故答案为:
| x |
| 1+2014x |
点评:本题考查逻辑推理中归纳推理,由特殊到一般进行归纳得出结论是此类推理方法的重要特征.

练习册系列答案
相关题目
在区间[-2,3]上随机选取一个数X,则X≤1的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
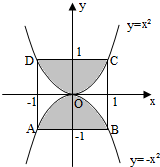 正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是
正方形的四个顶点A(-1,-1),B(1,-1),C(1,1),D(-1,1)分别在抛物线y=-x2和y=x2上,如图所示,若将一个质点随机投入正方形ABCD中,则质点落在图中阴影区域的概率是