题目内容
直线l1和l2是圆x2+y2=2的两条切线，若l1与l2的交点为（1，3），则l1与l2的夹角的正切值等于 ．
考点：两直线的夹角与到角问题
专题：直线与圆
分析：设l1与l2的夹角为2θ，由于l1与l2的交点A（1，3）在圆的外部，由直角三角形中的边角关系求得sinθ=
的值，可得cosθ、tanθ 的值，再根据tan2θ=
，计算求得结果．
| r |
| OA |
| 2tanθ |
| 1-tan2θ |
解答：
解：设l1与l2的夹角为2θ，由于l1与l2的交点A（1，3）在圆的外部，
且点A与圆心O之间的距离为OA=
=
，
圆的半径为r=
，
∴sinθ=
=
，
∴cosθ=
，tanθ=
=
，
∴tan2θ=
=
=
，
故答案为：
．
且点A与圆心O之间的距离为OA=
| 1+9 |
| 10 |
圆的半径为r=
| 2 |
∴sinθ=
| r |
| OA |
| ||
|
∴cosθ=
2
| ||
|
| sinθ |
| cosθ |
| 1 |
| 2 |
∴tan2θ=
| 2tanθ |
| 1-tan2θ |
| 1 | ||
1-
|
| 4 |
| 3 |
故答案为：
| 4 |
| 3 |
点评：本题主要考查直线和圆相切的性质，直角三角形中的变角关系，同角三角函数的基本关系、二倍角的正切公式的应用，属于中档题．
练习册系列答案
名题训练系列答案
期末集结号系列答案
相关题目
已知函数f（x）=
-log2x，在下列区间中，包含f（x）零点的区间是（ ）
| 6 |
| x |
| A、（0，1） |
| B、（1，2） |
| C、（2，4） |
| D、（4，+∞） |
学生的语文、数学成绩均被评定为三个等级，依次为“优秀”“合格”“不合格”．若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”．如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，则这一组学生最多有（ ）
| A、2人 | B、3人 | C、4人 | D、5人 |
正四棱锥的顶点都在同一球面上，若该棱锥的高为4，底面边长为2，则该球的表面积为（ ）
A、
| ||
| B、16π | ||
| C、9π | ||
D、
|
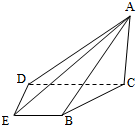如图，在四棱锥A-BCDE中，平面ABC⊥平面BCDE，∠CDE=∠BED=90°，AB=CD=2，DE=BE=1，AC=