题目内容
已知函数f(x)=
,若函数y=f(x)-kx有三个零点,则实数k的取值范围( )
|
| A、(0,1) | ||
B、(
| ||
| C、(-1,1) | ||
D、(
|
考点:分段函数的应用,函数零点的判定定理
专题:计算题,数形结合,函数的性质及应用
分析:分别求出x<0和x≥0时函数y=f(x)-kx零点的取值情况,利用数形结合切点和直线y=kx,k的取值范围即可得到.
解答:
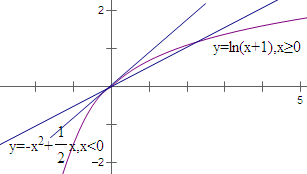 解:由y=f(x)-kx=0,得f(x)=kx
解:由y=f(x)-kx=0,得f(x)=kx
∵f(0)=ln1=0,
∴x=0是函数y=f(x)-kx的一个零点,
当x<0时,由f(x)=kx,
得-x2+
x=kx,
即-x+
=k,解得x=
-k,
由x=
-k<0,解得k>
,
当x>0时,函数f(x)=ln(x+1),
f'(x)=
∈(0,1),
∵x>0,
∴要使函数y=f(x)-kx在x>0时有一个零点,
则0<k<1,
∵k>
,
∴
<k<1,
即实数k的取值范围是(
,1),
故选:D.
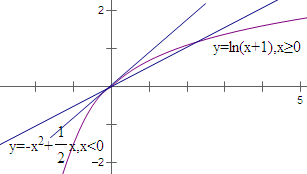 解:由y=f(x)-kx=0,得f(x)=kx
解:由y=f(x)-kx=0,得f(x)=kx∵f(0)=ln1=0,
∴x=0是函数y=f(x)-kx的一个零点,
当x<0时,由f(x)=kx,
得-x2+
| 1 |
| 2 |
即-x+
| 1 |
| 2 |
| 1 |
| 2 |
由x=
| 1 |
| 2 |
| 1 |
| 2 |
当x>0时,函数f(x)=ln(x+1),
f'(x)=
| 1 |
| x+1 |
∵x>0,
∴要使函数y=f(x)-kx在x>0时有一个零点,
则0<k<1,
∵k>
| 1 |
| 2 |
∴
| 1 |
| 2 |
即实数k的取值范围是(
| 1 |
| 2 |
故选:D.
点评:本题主要考查函数零点的个数的应用,利用方程和函数之间的关系,将函数零点转化为函数图象相交问题,利用数形结合是解决此类问题的关键,利用切线的临界位置是解决问题的突破点.

练习册系列答案
相关题目
下列命题中为真命题的是( )
| A、命题“若x2=1,则x=1” |
| B、命题“方程(x+2)2+(y-1)2=0的解为x=-2且y=1” |
| C、命题“若x<1,则x<0” |
| D、命题“若sinA=sinB,则A=B” |
已知动圆C与圆C1:x2+(y-2)2=9和圆C2:x2+(y+2)2=25都外切,则动圆圆心C的轨迹是( )
| A、圆 | B、椭圆 |
| C、双曲线 | D、双曲线的一支 |
下列函数中,值域为R的函数是( )
| A、f(x)=2x | ||
| B、f(x)=lg(tanx) | ||
C、f(x)=
| ||
| D、f(x)=|lnx| |
设直线l经过点(0,-2),且与圆x2+y2=1相切,则l的斜率是( )
| A、±1 | ||||
B、±
| ||||
C、±
| ||||
D、±
|