题目内容
已知椭圆C的中心在原点,焦点在x轴上,离心率e=
,它的一个顶点恰好是抛物线x2=-12y的焦点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C与曲线|y|=k•x(k>0)的交点为B、C,求△OBC面积的最大值.
| 1 |
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C与曲线|y|=k•x(k>0)的交点为B、C,求△OBC面积的最大值.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)求出抛物线的焦点,结合离心率e=
,及a,b,c的平方关系可求得椭圆C的方程;
(Ⅱ)设点A(x0,y0),(x0>0,y0>0),AB交x轴于点D,由对称性知S△OAB=2S△OAD,根据点A在直线OA、椭圆上可用k表示出x0,从而可把△OAB面积表示为关于k的函数,利用基本不等式即可求得其最大值.
| 1 |
| 2 |
(Ⅱ)设点A(x0,y0),(x0>0,y0>0),AB交x轴于点D,由对称性知S△OAB=2S△OAD,根据点A在直线OA、椭圆上可用k表示出x0,从而可把△OAB面积表示为关于k的函数,利用基本不等式即可求得其最大值.
解答:
解:(Ⅰ)抛物线x2=-12y的焦点为(0,-3),∴b=3 …(1分)
又椭圆离心率e=
=
,∴a2=9+
a2,∴a2=12…(2分)
所以椭圆C的方程为
+
=1 …(4分)
(Ⅱ)设点A(x0,y0),(x0>0,y0>0),则y0=kx0,
设AB交x轴于点D,由对称性知:
S△OAB=2S△OAD=2×
x0y0=kx02,
由y0=kx0,代入椭圆方程,可得x02=
,
所以S△OAB=k•
=
≤
=3
,
当且仅当
=4k,即k=
时取等号,
所以△OAB面积的最大值为3
.
又椭圆离心率e=
| c |
| a |
| 1 |
| 2 |
| 1 |
| 4 |
所以椭圆C的方程为
| x2 |
| 12 |
| y2 |
| 9 |
(Ⅱ)设点A(x0,y0),(x0>0,y0>0),则y0=kx0,
设AB交x轴于点D,由对称性知:
S△OAB=2S△OAD=2×
| 1 |
| 2 |
由y0=kx0,代入椭圆方程,可得x02=
| 36 |
| 3+4k2 |
所以S△OAB=k•
| 36 |
| 3+4k2 |
| 36 | ||
|
| 36 | ||||
2
|
| 3 |
当且仅当
| 3 |
| k |
| ||
| 2 |
所以△OAB面积的最大值为3
| 3 |
点评:本题考查直线与圆锥曲线的位置关系及椭圆方程的求解,考查函数思想,解决(Ⅱ)问的关键是把三角形OAB面积表示为函数,正确运用基本不等式是解决基础.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知直线l1:3x+2ay-5=0,l2:(3a-1)x-ay-2=0,若l1∥l2,则a的值为( )
A、-
| ||
| B、6 | ||
| C、0 | ||
D、0或-
|
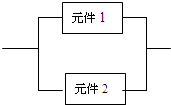 某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为
某个部件由两个电子元件按如图连接而成,当元件1或元件2正常工作,该部件正常工作.设两个电子元件的使用寿命(单位:小时)均服从正态分布N(800,100),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过800小时的概率为