题目内容
已知公比为负值的等比数列{an}中,a1a5=4,a4=-1.
(1)求数列{an}的通项公式;
(2)设bn=
+
+…+
,求数列{an+bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)设bn=
| n+1 |
| 1×2 |
| n+1 |
| 2×3 |
| n+1 |
| n(n+1) |
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)设等比数列{an}的公比为q<0,由a1a5=4,a4=-1.可得
q4=4,a1q3=-1,解得即可;
(2)由bn=
+
+…+
=(n+1)[(1-
)+(
-
)+…+(
-
)]=n,可得an+bn=
+n,再利用等差数列与等比数列的前n项和公式即可得出.
| a | 2 1 |
(2)由bn=
| n+1 |
| 1×2 |
| n+1 |
| 2×3 |
| n+1 |
| n(n+1) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 8 |
| (-2)n-1 |
解答:
解:(1)设等比数列{an}的公比为q<0,
∵a1a5=4,a4=-1.
∴
q4=4,a1q3=-1,解得q=-
,a1=8.
∴an=8×(-
)n-1=
.
(2)∵bn=
+
+…+
=(n+1)[(1-
)+(
-
)+…+(
-
)]
=(n+1)×(1-
)=n,
∴an+bn=
+n,
其前n项和Sn=8×
+
=
[1-(-
)n]+
.
∵a1a5=4,a4=-1.
∴
| a | 2 1 |
| 1 |
| 2 |
∴an=8×(-
| 1 |
| 2 |
| 8 |
| (-2)n-1 |
(2)∵bn=
| n+1 |
| 1×2 |
| n+1 |
| 2×3 |
| n+1 |
| n(n+1) |
=(n+1)[(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=(n+1)×(1-
| 1 |
| n+1 |
∴an+bn=
| 8 |
| (-2)n-1 |
其前n项和Sn=8×
1-(-
| ||
1-(-
|
| n(n+1) |
| 2 |
| 16 |
| 3 |
| 1 |
| 2 |
| n(n+1) |
| 2 |
点评:本题考查了等差数列与等比数列的通项公式及其前n项和公式、“裂项求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
若函数f(x)=
的值域为R,则m的取值范围是( )
| x |
| mx2+mx+1 |
| A、[0,4] |
| B、(-∞,0) |
| C、(-∞,0] |
| D、(-∞,0]∪[4,+∞) |
已知向量
=(-a,2,1)与
=(1,2a,-3)垂直,则a等于( )
| m |
| n |
| A、2 | B、-2 | C、1 | D、-1 |
空间中,对于平面α和共面的两直线m、n,下列命题中为真命题的是( )
| A、若m⊥α,m⊥n,则n∥α |
| B、若m∥α,n∥α,则m∥n |
| C、若m、n与α所成的角相等,则m∥n |
| D、若m?α,n∥α,则m∥n |
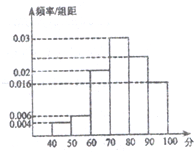 从某校高三学生中抽取n名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40,100),且成绩在区间[70,90)的学生人数是27人.
从某校高三学生中抽取n名学生参加数学竞赛,根据成绩(单位:分)的分组及各数据绘制的频率分布直方图如图所示,已知成绩的范围是区间[40,100),且成绩在区间[70,90)的学生人数是27人.