题目内容
已知函数f(x)=
x3-ax2-2ax,其中a∈R.
(Ⅰ)若x=1是函数f(x)的极值点,求a的值;
(Ⅱ)若f(x)在区间(2,+∞)上单调递增,求a的取值范围.
| 2 |
| 3 |
(Ⅰ)若x=1是函数f(x)的极值点,求a的值;
(Ⅱ)若f(x)在区间(2,+∞)上单调递增,求a的取值范围.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)利用x=1时的导数为0列方程,解出a的值;
(2)由已知f′(x)≥0在(2,+∞)上恒成立,只需分离a,然后构造函数,求其最小(大)值即可.
(2)由已知f′(x)≥0在(2,+∞)上恒成立,只需分离a,然后构造函数,求其最小(大)值即可.
解答:
解:(Ⅰ)由f(x)=
x3-ax2-2ax,得f′(x)=2x2-2ax-2a.
因为x=1是函数f(x)的极值点,
所以f′(1)=2-2a-2a=0,解得a=
.
经检验x=1为函数f(x)的极值点,
所以a=
.
(Ⅱ)∵f(x)在区间(2,+∞)上单调递增,
∴f'(x)=2x2-2ax-2a≥0在区间(2,+∞)上恒成立,
∴a≤
对区间x∈(2,+∞)恒成立,
令g(x)=
,则g'(x)=
=
∴当x∈(2,+∞)时,g'(x)>0,有g(x)=
>g(2)=
,
∴a的取值范围为(-∞,
].
| 2 |
| 3 |
因为x=1是函数f(x)的极值点,
所以f′(1)=2-2a-2a=0,解得a=
| 1 |
| 2 |
经检验x=1为函数f(x)的极值点,
所以a=
| 1 |
| 2 |
(Ⅱ)∵f(x)在区间(2,+∞)上单调递增,
∴f'(x)=2x2-2ax-2a≥0在区间(2,+∞)上恒成立,
∴a≤
| x2 |
| x+1 |
令g(x)=
| x2 |
| x+1 |
| 2x(x+1)-x2 |
| (x+1)2 |
| x2+2x |
| (x+1)2 |
∴当x∈(2,+∞)时,g'(x)>0,有g(x)=
| x2 |
| x+1 |
| 4 |
| 3 |
∴a的取值范围为(-∞,
| 4 |
| 3 |
点评:本题考查了利用导数研究函数的极值、单调性的问题.后者一般转化为函数的最值问题,能分离参数的尽量分离.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
函数函数y=
的定义域是( )
| lg(3x+1) | ||
|
| A、∅ | ||
B、(-
| ||
C、(-
| ||
D、(-∞,-
|
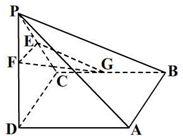 如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,点E,F,G分别为PC,PD,BC的中点.
如图所示,四棱锥P-ABCD中,底面ABCD为正方形,PD⊥平面ABCD,PD=AB=2,点E,F,G分别为PC,PD,BC的中点.