题目内容
2.已知函数f(x)=alnx-bx2,a,b∈R.若f(x)在x=1处与直线y=-$\frac{1}{2}$相切.(1)求a,b的值;
(2)求f(x)在[$\frac{1}{e}$,e]上的最大值.
分析 (1)对f(x)进行求导,f′(x)欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.列出关于a,b的方程求得a,b的值.
(2)研究闭区间上的最值问题,先求出函数的极值,比较极值和端点处的函数值的大小,最后确定出最大值.
解答 解:(1)∵函数f(x)=alnx-bx2(x>0),∴f′(x)=$\frac{a}{x}$-2bx,
∵函数f(x)在x=1处与直线y=-$\frac{1}{2}$相切,
∴$\left\{\begin{array}{l}{f′(1)=a-2b=0}\\{f(1)=-b=-\frac{1}{2}}\end{array}\right.$,解得 $\left\{\begin{array}{l}{a=1}\\{b=\frac{1}{2}}\end{array}\right.$;
(2)f(x)=lnx-$\frac{1}{2}$x2,f′(x)=$\frac{1{-x}^{2}}{x}$,
当$\frac{1}{e}$≤x≤e时,令f'(x)>0得:$\frac{1}{e}$≤x<1,
令f'(x)<0,得1<x≤e,
∴f(x)在[$\frac{1}{e}$,1],上单调递增,
在[1,e]上单调递减,
∴f(x)max=f(1)=-$\frac{1}{2}$.
点评 本小题主要考查函数单调性的应用、利用导数研究曲线上某点切线方程、导数在最大值、最小值问题中的应用、不等式的解法等基础知识,考查运算求解能力、化归与转化思想.属于中档题.

练习册系列答案
相关题目
12.设α,β是两个不同的平面,m,n是两条不同的直线,给出下列四个论断①m∥n;②α∥β③m⊥α;④n⊥β.以其中三个论断作为条件,余下一个论断作为结论,则一共可以写出真命题的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.cos35°cos25°-sin145°cos65°的值为( )
| A. | -$\frac{1}{2}$ | B. | cos10° | C. | $\frac{1}{2}$ | D. | -cos10° |
10.下列函数在(0,+∞)上是增函数的是( )
| A. | y=3-x | B. | y=-2x | C. | y=log0.1x | D. | y=x${\;}^{\frac{1}{2}}$ |
17.已知集合A={第一象限角},B={锐角},C={小于90°的角},下面关系正确( )
| A. | A=B=C | B. | A⊆C | C. | A∩C=B | D. | B⊆A∩C |
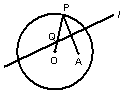 如图,圆O的半径为定长r,A是圆O内的一定点,P为圆上任意 一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆周上运动时,点Q的轨迹是( )
如图,圆O的半径为定长r,A是圆O内的一定点,P为圆上任意 一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆周上运动时,点Q的轨迹是( ) (1)某简单几何体的三视图中,正视图、侧视图、俯视图都是如图所示的直角边长为1的等腰直角三角形,求该几何体的表面积和体积;
(1)某简单几何体的三视图中,正视图、侧视图、俯视图都是如图所示的直角边长为1的等腰直角三角形,求该几何体的表面积和体积;