题目内容
6.将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论:?①AC⊥BD;?
②△ACD是等边三角形;
?③AB与平面BCD成60°的角;
④AB与CD所成的角是90°.
其中正确结论的序号是①②.
分析 由题意画出图形,然后利用线面垂直的判定和性质判断①;求出AC长度判断②;由图求得AB与平面BCD所成角判断③;利用反证法说明④错误.
解答 解:如图,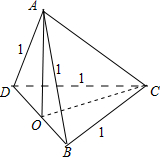
设正方形ABCD的边长为1,BD中点为O,连接AO,CO,
则AO⊥BD,CO⊥BD,∴BD⊥平面AOC,则AC⊥BD,故①正确;
由平面ABD⊥平面BCD,且AO⊥BD,得AO⊥平面BCD,
∴AO⊥CO,则AC=$\sqrt{(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{2}}{2})^{2}}=1$,则△ACD是等边三角形,故②正确;
AB与平面BCD所成角为∠ABO=45°,故③错误;
若AB与CD所成的角是90°,即AB⊥CD,又AO⊥CD,∴CD⊥平面ADB,而CO⊥平面ADB,故④错误.
∴正确结论的序号是①②.
故答案为:①②.
点评 本题考查空间中位置关系的判定,考查空间想象能力和思维能力,是中档题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
6.设集合A={0,1,2},B={1,2},则( )
| A. | A=B | B. | A∩B=∅ | C. | A⊆B | D. | A?B |
11.命题p:?x0∈R,x02-x0+1≤0的否定是( )
| A. | ?x∈R,x2-x+1>0 | B. | ?x∈R,x2-x+1≤0 | ||
| C. | ?x0∈R,x02-x0+1>0 | D. | ?x0∈R,x02-x0+1<0 |
 如图,已知在三棱柱ABC-A1B1C1中,B1B⊥平面ABC,AB⊥BC,AB=BC=BB1=2.
如图,已知在三棱柱ABC-A1B1C1中,B1B⊥平面ABC,AB⊥BC,AB=BC=BB1=2.