题目内容
已知函数f(x)=x2-ax+
,x∈[0,1],求f(x)的最小值g(a)的表达式,并求出g(a)的最大值.
| a |
| 2 |
考点:二次函数在闭区间上的最值
专题:函数的性质及应用
分析:根据函数f(x)=(x-
)2+
-
,x∈[0,1],利用二次函数的性质、分类讨论求得f(x)的最小值g(a),再画出函数g(a)的图象,数形结合求得g(a)的最大值.
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
解答:
 解:∵函数f(x)=x2-ax+
解:∵函数f(x)=x2-ax+
=(x-
)2+
-
,x∈[0,1],
∴当
∈[0,1]时,f(x)的最小值g(a)=f(
)=
-
;
当
<0时,函数f(x)在[0,1]上增函数,f(x)的最小值g(a)=f(0)=
;
当
>1时,函数f(x)在[0,1]上减函数,f(x)的最小值g(a)=f(1)=1-
.
综上可得,g(a)=
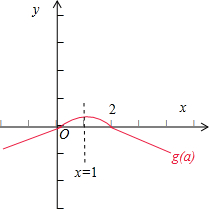
,画出函数g(a)的图象,如图所示:
显然,函数g(a)在x=1处取得最大值为g(1)=
.
 解:∵函数f(x)=x2-ax+
解:∵函数f(x)=x2-ax+| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
∴当
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
当
| a |
| 2 |
| a |
| 2 |
当
| a |
| 2 |
| a |
| 2 |
综上可得,g(a)=
|
显然,函数g(a)在x=1处取得最大值为g(1)=
| 1 |
| 4 |
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了数形结合、分类讨论的数学思想,属基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
不等式||x|-1|≤2的解集为( )
| A、[-3,3] |
| B、[-1,3] |
| C、[-3,1] |
| D、[-1,1] |
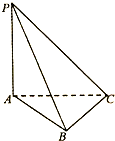 如图,在三棱锥P-ABC中,已知△ABC是等腰直角三角形,∠ABC=90°,△PAC是直角三角形,∠PAC=90°,∠ACP=30°,平面PAC⊥平面ABC.
如图,在三棱锥P-ABC中,已知△ABC是等腰直角三角形,∠ABC=90°,△PAC是直角三角形,∠PAC=90°,∠ACP=30°,平面PAC⊥平面ABC.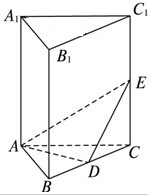 已知在直三棱柱ABC-A1B1C1中,E为CC1上任意一点,D在BC上(点D不同于点C),AD⊥DE,求证:平面ADE⊥平面BCC1B1.
已知在直三棱柱ABC-A1B1C1中,E为CC1上任意一点,D在BC上(点D不同于点C),AD⊥DE,求证:平面ADE⊥平面BCC1B1.