Question

18．已知三棱锥O-ABC中，A、B、C三点在以O为球心的球面上，若AB=BC=1，∠ABC=120°，三棱锥O-ABC的体积为$\frac{\sqrt{5}}{4}$，则球O的表面积为（　　）

• A． $\frac{32}{3}$π
• B． 16π
• C． 64π
• D． 544π

Answer 1

分析 求出底面三角形的面积，利用三棱锥的体积求出O到底面的距离，求出底面三角形的所在平面圆的半径，通过勾股定理求出球的半径，即可求解球的体积．

解答 解：三棱锥O-ABC，A、B、C三点均在球心O的表面上，且AB=BC=1，∠ABC=120°，AC=$\sqrt{3}$，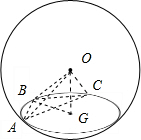

∴S_△ABC=$\frac{1}{2}×1×1×sin120°$=$\frac{\sqrt{3}}{4}$，
∵三棱锥O-ABC的体积为$\frac{\sqrt{5}}{4}$，△ABC的外接圆的圆心为G，∴OG⊥⊙G，
外接圆的半径为：GA=$\frac{\sqrt{3}}{2sin120°}$=1，
∴$\frac{1}{3}×\frac{\sqrt{3}}{4}×$OG=$\frac{\sqrt{5}}{4}$，
∴OG=$\sqrt{15}$，
球的半径为：$\sqrt{15+1}$=4．
球的表面积：4π4²=64π．
故选：C．

点评 本题考查球的表面积的求法，球的内含体与三棱锥的关系，考查空间想象能力以及计算能力．