题目内容
6.若函数f(x)是一次函数,且f(f(x))=4x+1,则f(x)=$2x+\frac{1}{3},或-2x-1$.分析 由题意,设出f(x)=kx+b,利用待定系数法求解即可.
解答 解:函数f(x)是一次函数,设f(x)=kx+b,(k≠0)
f(f(x))=kf(x)+b=k2x+kb+b.
∵f(f(x))=4x+1,即k2x+kb+b=4x+1,
由$\left\{\begin{array}{l}{{k}^{2}=4}\\{kb+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{b=\frac{1}{3}}\end{array}\right.$或$\left\{\begin{array}{l}{b=-2}\\{b=-1}\end{array}\right.$
∴f(x)=$2x+\frac{1}{3},或-2x-1$.
故答案为:$2x+\frac{1}{3},或-2x-1$.
点评 本题考查了函数解析式的求法,利用了待定系数法.属于基础题.

练习册系列答案
相关题目
7.设g(x)为定义在R上的奇函数,且g(x)不恒为0,若$f(x)=(\frac{1}{{{a^x}-1}}-\frac{1}{b})g(x)$(a>0且a≠1)为偶函数,则常数b=( )
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
1.已知三角形ABC的顶点都在半径为R的球O的球面上,AB⊥BC,AB=6,BC=8,棱锥O-ABC的体积为40,则球的表面积为( )
| A. | 250π | B. | 200π | C. | 100π | D. | 50π |
18.已知三棱锥O-ABC中,A、B、C三点在以O为球心的球面上,若AB=BC=1,∠ABC=120°,三棱锥O-ABC的体积为$\frac{\sqrt{5}}{4}$,则球O的表面积为( )
| A. | $\frac{32}{3}$π | B. | 16π | C. | 64π | D. | 544π |
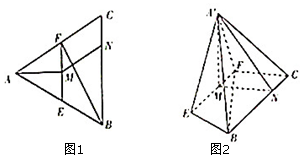 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.