题目内容
9. 如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,则△ADC的面积S为$\frac{3+\sqrt{3}}{2}$.
如图,平面四边形ABCD中,AB=$\sqrt{5}$,AD=2$\sqrt{2}$,CD=$\sqrt{3}$,∠CBD=30°,∠BCD=120°,则△ADC的面积S为$\frac{3+\sqrt{3}}{2}$.
分析 在△BCD中由正弦定理解出BD,在△ABD中,由余弦定解出∠ADB的度数;代入三角形的面积公式计算.
解答 解:在△BCD中,由正弦定理得:$\frac{BD}{sin∠BCD}$=$\frac{CD}{sin∠CBD}$,
即 $\frac{BD}{\frac{\sqrt{3}}{2}}$=$\frac{\sqrt{3}}{\frac{1}{2}}$,解得BD=3.
在△ABD中,由余弦定理得:cos∠ADB=$\frac{{AD}^{2}{+BD}^{2}{-AB}^{2}}{2AD•BD}$=$\frac{\sqrt{2}}{2}$
∴∠ADB=45°.
∵∠CBD=30°,∠BCD=120°,∴∠CDB=30°.
∴sin∠ADC=sin(45°+30°)=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∴S△ACD=$\frac{1}{2}$•AD•CDsin∠ADC=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{3}$×$\frac{\sqrt{6}+\sqrt{2}}{4}$=$\frac{{3+\sqrt{3}}}{2}$,
故答案为:$\frac{3+\sqrt{3}}{2}$.
点评 本题考查了正余弦定理在解三角形中的应用,属于中档题.

练习册系列答案
相关题目
4.已知sinα+cosα=$\frac{\sqrt{3}}{2}$,且α∈(0,π),则sin2α的值为( )
| A. | -$\frac{\sqrt{15}}{4}$ | B. | -$\frac{1}{4}$ | C. | $\frac{\sqrt{15}}{4}$ | D. | $\frac{1}{4}$ |
1.已知三角形ABC的顶点都在半径为R的球O的球面上,AB⊥BC,AB=6,BC=8,棱锥O-ABC的体积为40,则球的表面积为( )
| A. | 250π | B. | 200π | C. | 100π | D. | 50π |
18.已知三棱锥O-ABC中,A、B、C三点在以O为球心的球面上,若AB=BC=1,∠ABC=120°,三棱锥O-ABC的体积为$\frac{\sqrt{5}}{4}$,则球O的表面积为( )
| A. | $\frac{32}{3}$π | B. | 16π | C. | 64π | D. | 544π |
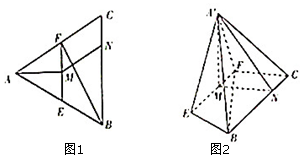 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,M为EF的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A'EF的位置,使平面A'EF⊥平面EFCB.