题目内容
(Ⅰ)已知a和b是任意非零实数.证明:
≥4;
(Ⅱ)若不等式|2x+1|-|x+1|>k(x-1)-
恒成立,求实数k的取值范围.
| |2a+b|+|2a-b| |
| |a| |
(Ⅱ)若不等式|2x+1|-|x+1|>k(x-1)-
| 1 |
| 4 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:(Ⅰ)利用双绝对值不等式的性质|2a+b|+|2a-b|≥|2a+b+2a-b|=4|a|即可证得结论成立;
(Ⅱ)构造函数h(x)=|2x+1|-|x+1|=
,作出y=h(x)与过定点(1,-
)的直线y=k(x-1)-
的图象,数形结合即可求得实数k的取值范围.
(Ⅱ)构造函数h(x)=|2x+1|-|x+1|=
|
| 1 |
| 4 |
| 1 |
| 4 |
解答:
证明:(Ⅰ)|2a+b|+|2a-b|≥|2a+b+2a-b|=4|a|
∴
≥4.
(Ⅱ)记h(x)=|2x+1|-|x+1|=
若不等式|2x+1|-|x+1|>k(x-1)-
恒成立,
则函数h(x)的图象在直线y=k(x-1)-
的上方,
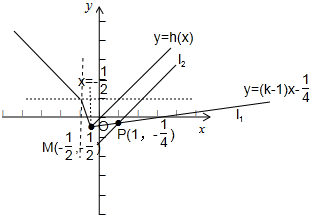
∵y=k(x-1)-
经过定点(1,-
),当x=-
时,y=h(x)取得最小值-
,
显然,当y=k(x-1)-
经过定点P(1,-
)与M(-
,-
)时,kPM=
=
,即k>
;
当y=k(x-1)-
经过定点P(1,-
)与直线y=x平行时,k得到最大值1,
∴k∈(
,1].
∴
| |2a+b|+|2a-b| |
| |a| |
(Ⅱ)记h(x)=|2x+1|-|x+1|=
|
若不等式|2x+1|-|x+1|>k(x-1)-
| 1 |
| 4 |
则函数h(x)的图象在直线y=k(x-1)-
| 1 |
| 4 |

∵y=k(x-1)-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
显然,当y=k(x-1)-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
-
| ||||
1-(-
|
| 1 |
| 6 |
| 1 |
| 6 |
当y=k(x-1)-
| 1 |
| 4 |
| 1 |
| 4 |
∴k∈(
| 1 |
| 6 |
点评:本题考查函数恒成立问题,着重考查绝对值不等式的性质,突出构造函数思想与数形结合思想的应用,考查转化思想与运算求解能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合S={x|x2-2x=0x∈R},T={x|x2+2x-3≤0,x∈R},则S∩T=( )
| A、{0,2} |
| B、{0} |
| C、{0,-2} |
| D、{2,0,-2} |
已知集合M={x||x|<2},N={x|-1≤x≤3},M∪N=( )
| A、{-1,2} |
| B、[-1,2) |
| C、{-2,3} |
| D、(-2,3] |
