题目内容
8.观察如图算式:23=3+5;
33=7+9+11;
43=13+15+17+19;
53=21+23+25+27+29
…
203=a1+a2+a3+…,其中a1<a2<a3<…,那么a1=381.
分析 可得规律:第n行的左边是n3,右边是n个连续奇数的和,设第n行的第一个数为an,累加可得an,计算可得a20.
解答 解:由题意可得第n行的左边是n3,右边是n个连续奇数的和,
设第n行的第一个数为an,则有a2-a1=3-1=2,
a3-a2=7-3=4,…an-an-1=2(n-1),
以上(n-1)个式子相加可得an-a1=$\frac{(n-1)[2+2(n-1)]}{2}$,
故an=n2-n+1,
∴a20=202-20+1=381.
故答案为:381.
点评 本题考查归纳推理,涉及累加法求数列的通项公式,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.函数y=x+$\frac{4}{x}$的单调递增区间为( )
| A. | (-2,0)∪(0,2) | B. | (-∞,-2)∪(2,+∞) | C. | (-2,0),(0,2) | D. | (-∞,-2),(2,+∞) |
13.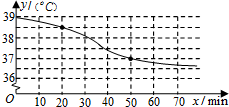 现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
 现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )
现对复方氨酚烷胺片(中文名:感康)进行深入临床观察,该药物随着进入病人体内的时间与体温的变化情况如图所示,则当时间x从20min到50min时,体温y相对于时间x的平均变化率为( )| A. | 0.05(℃/min) | B. | -0.05(℃/min) | C. | 0.025(℃/min) | D. | -0.025(℃/min) |
17.若x>1,则函数y=x+$\frac{4}{x-1}$的最小值为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
18.下面四个图象中,符合函数y=-xsinx的图象是( )
| A. |  | B. |  | C. |  | D. |  |