题目内容
4.f(x)=$\left\{\begin{array}{l}{\frac{\sqrt{x+1}-1}{x},x≠0}\\{0,x=0}\end{array}\right.$,则x=0是( )| A. | 可去间断点 | B. | 无穷间断点 | C. | 连续点 | D. | 跳跃间断点 |
分析 由x≠0时,f(x)=$\frac{\sqrt{x+1}-1}{x}$=$\frac{1}{\sqrt{x+1}+1}$,可得x→0时,f(x)→$\frac{1}{2}$≠0,即可判断出结论.
解答 解:x≠0时,f(x)=$\frac{\sqrt{x+1}-1}{x}$=$\frac{1}{\sqrt{x+1}+1}$,
∴x→0时,f(x)→$\frac{1}{2}$≠0,
因此x=0是函数f(x)跳跃间断点.
故选:D.
点评 本题考查了函数的化简、有理化因式、极限性质、函数的连续性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.数列{an}中,已知a1=1,S2=2,且Sn+1+2Sn-1=3Sn(n≥2,n∈N*),则数列{an}为( )
| A. | 等差数列 | B. | 等比数列 | ||
| C. | 从第二项起为等差数列 | D. | 从第二项起为等比数列 |
13.${∫}_{-2}^{-1}$$\frac{2}{x}$dx=( )
| A. | -ln2 | B. | ln2 | C. | -2ln2 | D. | 2ln2 |
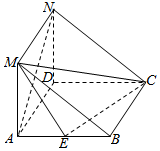 如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.
如图,在三棱柱ABM-DCN中,侧面ADNM⊥侧面ABCD,且侧面ABCD是菱形,∠DAB=60°,AD=2,侧面ADNM是矩形,AM=1.E是AB的中点.